Reflection Triangle
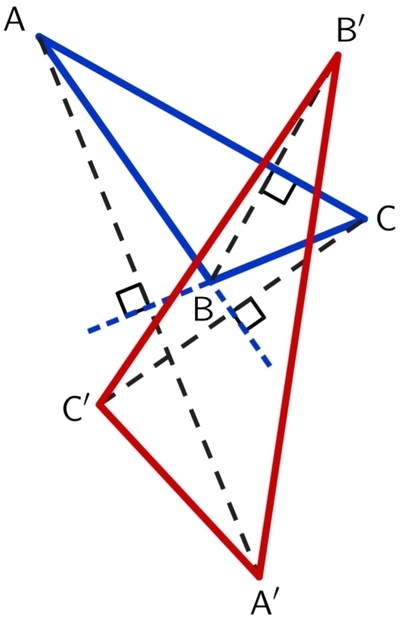 The vertices of a triangle
are reflected about the opposite sides, and the resulting points form the vertices of the 'reflection' triangle
.
The vertices of a triangle
are reflected about the opposite sides, and the resulting points form the vertices of the 'reflection' triangle
.
Let the areas of and be and respectively.
There are only three which are similar to their respective reflection triangles , two of which are: the equilateral triangle and the heptagonal triangle .
Find for the third such triangle.
Note: is the golden ratio .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
where we write u = a 2 , v = b 2 , w = c 2 . Putting u = 1 we obtain 2 w + v − 1 = 2 v + v w − v 2 = 2 v w + w − w 2 so that v = 2 and w = v − 2 v 2 − v − 1 and 2 ( v − 2 v 2 − v − 1 ) + v − 1 f ( v ) = ( 2 v + 1 ) v − 2 v 2 − v − 1 − ( v − 2 v 2 − v − 1 ) 2 = v 4 − 6 v 3 + 1 1 v 2 − 7 v + 1 = v ( v − 2 ) 3 − ( v 2 − v − 1 ) = 0 which implies that w = v ( v − 2 ) 2 . We also note that f ( v ) = ( v − 1 ) ( v 3 − 5 v 2 + 6 v − 1 ) = ( v − 1 ) g ( v ) . Thus we obtain an acceptable triple ( u , v , w ) = ( 1 , v , v ( v − 2 ) 2 ) provided that f ( v ) = 0 . There are two cases:
Life is more complicated in general, and we need to adopt a more algebraically intense approach. The formulae we derived above for distances such as A N C now have to be treated as signed distances, but we can still use the Cosine Rules to obtain expressions for the lengths α , β , γ of the sides of the pedal triangle N A N B N C . These can most easily be expressed in terms of u = a 2 , v = b 2 , w = c 2 , and if we write U = α 2 , V = β 2 , W = γ 2 , we obtain U = 1 6 v w P V = 1 6 u w Q W = 1 6 u v R where P Q R = ( u − v ) 3 + ( u − w ) 3 + v w ( 3 u + v + w ) − u 3 = ( v − u ) 3 + ( v − w ) 3 + u w ( u + 3 v + w ) − v 3 = ( w − u ) 3 + ( w − v ) 3 + u v ( u + v + 3 w ) − w 3 and we want to solve v U = w V = u W = λ 2 . We see that u , v , w must satisfy the polynomial equations u v Q − w 2 R = u w P − v 2 Q = 0 . Scaling so that u = 1 we obtain the polynomial identities A 1 ( v , w ) = ( u v Q − w 2 R ) ∣ ∣ ∣ u = 1 = 0 A 2 ( v , w ) = ( u w P − v 2 Q ) ∣ ∣ ∣ u = 1 = 0 As polynomials in w , A 1 is quintic and A 2 quartic, and both have leading coefficient − 1 . We can readily divide A 2 ( v , w ) into A 1 ( v , w ) . The remainder has a factor of v , and we can write
A 1 ( v , X ) − ( X + v 2 − 2 v ) A 2 ( v , X ) ≡ v A 3 ( v , X ) where A 3 ( v , X ) is a cubic polynomial in X with leading term − p 3 ( v ) X 3 = − ( v 3 − 4 v 2 + 4 v + 1 ) X 3 . The polynomial p 3 ( X ) has no positive real zeroes, and so p 3 ( v ) = 0 . We have the identity A 3 ( v , w ) = 0 Continuing the polynomial division, we can write p 3 ( v ) 2 A 2 ( v , X ) ≡ [ p 3 ( v ) X − v 5 + 6 v 4 − 1 2 v 3 + 9 v 2 − 4 v − 6 ] A 3 ( v , X ) − 2 A 4 ( v , X ) where A 4 ( v , X ) ≡ ( 3 v 6 − 1 6 v 5 + 1 1 v 4 + 4 5 v 3 − 5 0 v 2 − 7 v + 1 2 ) X 2 − ( 3 v 7 − 1 8 v 6 + 2 9 v 5 − 9 v 4 + 6 v 3 − 1 7 v 2 − 6 v + 1 0 ) X + ( v 8 − 7 v 7 + 1 4 v 6 + v 5 − 3 4 v 4 + 3 7 v 3 − 8 v 2 − 7 v + 3 ) ≡ p 4 ( v ) X 2 + q 4 ( v ) X + r 4 ( X ) and we must have A 4 ( v , w ) = 0 . If p 4 ( v ) = 0 then (since p 4 ( X ) and q 4 ( X ) are coprime) we see that q 4 ( v ) = 0 , so we must have w = − q 4 ( v ) r 4 ( v ) , and hence 0 = A 3 ( v , − q 4 ( v ) r 4 ( v ) ) = q 4 ( v ) 3 P ( v ) for some polynomial P ( X ) of degree 2 7 . But this is impossible, since it can be shown that P ( X ) and p 4 ( X ) are coprime. Thus we deduce that p 4 ( v ) = 0 . Performing one more polynomial division, we can show that the remainder when A 3 ( v , X ) is divided by A 4 ( v , X ) is A 5 ( v , X ) ≡ p 4 ( v ) 2 ( v − 1 ) p 3 ( v ) 2 [ − ( 6 v 1 0 − 4 1 v 9 + 5 9 v 8 + 7 0 v 7 − v 6 − 5 2 0 v 5 + 5 0 1 v 4 + 7 4 v 3 − 1 2 9 v 2 − 1 5 v + 8 ) X + ( v − 1 ) 3 ( 3 v 8 − 1 8 v 7 + 1 2 v 6 + 7 3 v 5 − 6 1 v 4 − 8 0 v 3 + 4 8 v 2 + 1 7 v − 6 ) ] ≡ p 4 ( v ) 2 ( v − 1 ) p 3 ( v ) 2 [ p 5 ( v ) X + q 5 ( v ) ] where the polynomials p 5 ( X ) and q 5 ( X ) are coprime, and again we must have A 5 ( v , w ) = 0 .
If v = 1 we must have A 4 ( 1 , w ) = 2 w ( 1 − w ) = 0 , and hence w = 1 . Thus we obtain an equilateral triangle in this case.
Assume now that v = 1 . We know that p 3 ( v ) = 0 , so we deduce that p 5 ( v ) w + q 5 ( v ) = 0 . Since p 5 and q 5 are coprime, we cannot have p 5 ( v ) = q 5 ( v ) = 0 . Thus p 5 ( v ) = 0 , and w = − p 5 ( v ) q 5 ( v ) = 6 v 1 0 − 4 1 v 9 + 5 9 v 8 + 7 0 v 7 − v 6 − 5 2 0 v 5 + 5 0 1 v 4 + 7 4 v 3 − 1 2 9 v 2 − 1 5 v + 8 ( v − 1 ) 3 ( 3 v 8 − 1 8 v 7 + 1 2 v 6 + 7 3 v 5 − 6 1 v 4 − 8 0 v 3 + 4 8 v 2 + 1 7 v − 6 ( ⋆ ) But this implies that 0 = A 4 ( v , − p 5 ( v ) q 5 ( v ) ) p 5 ( v ) 2 = ( v − 1 ) 5 p 4 ( v ) 2 ( v 2 + v + 1 ) ( v 3 − 5 v 2 + 6 v − 1 ) ( v 6 − 2 v 5 − 1 3 v 4 + 3 2 v 3 − 9 v 2 − 6 v + 1 )
We have excluded the case v = 1 , and we know that p 4 ( v ) is nonzero. The polynomial 1 + v + v 2 is never zero for real v . As we have seen above, the case v 3 − 5 v 2 + 6 v − 1 = 0 leads to the heptagonal triangle. The remaining factor v 6 − 2 v 5 − 1 3 v 4 + 3 2 v 3 − 9 v 2 − 6 v + 1 = ( v 3 − v 2 + 3 v − 1 ) 2 − 2 0 ( v 2 − v ) 2 factorizes as ( v 3 − ( 1 + 2 5 ) v 2 + ( 3 + 2 5 ) v − 1 ) ( v 3 + ( 2 5 − 1 ) v 2 + ( 3 − 2 5 ) v − 1 ) Two of the zeros of the second cubic are negative, and the third zero gives a negative value of w , so we are left with investigating the case when v satisfies v 3 − ( 1 + 2 5 ) v 2 + ( 3 + 2 5 ) v − 1 = 0
Another fit of polynomial division:
And finally:
In the diagram below, the left-hand triangle is the heptagonal triangle, and the right-hand triangle is the new one.