Reflections from the surface of an ellipse

Calculus Level 2

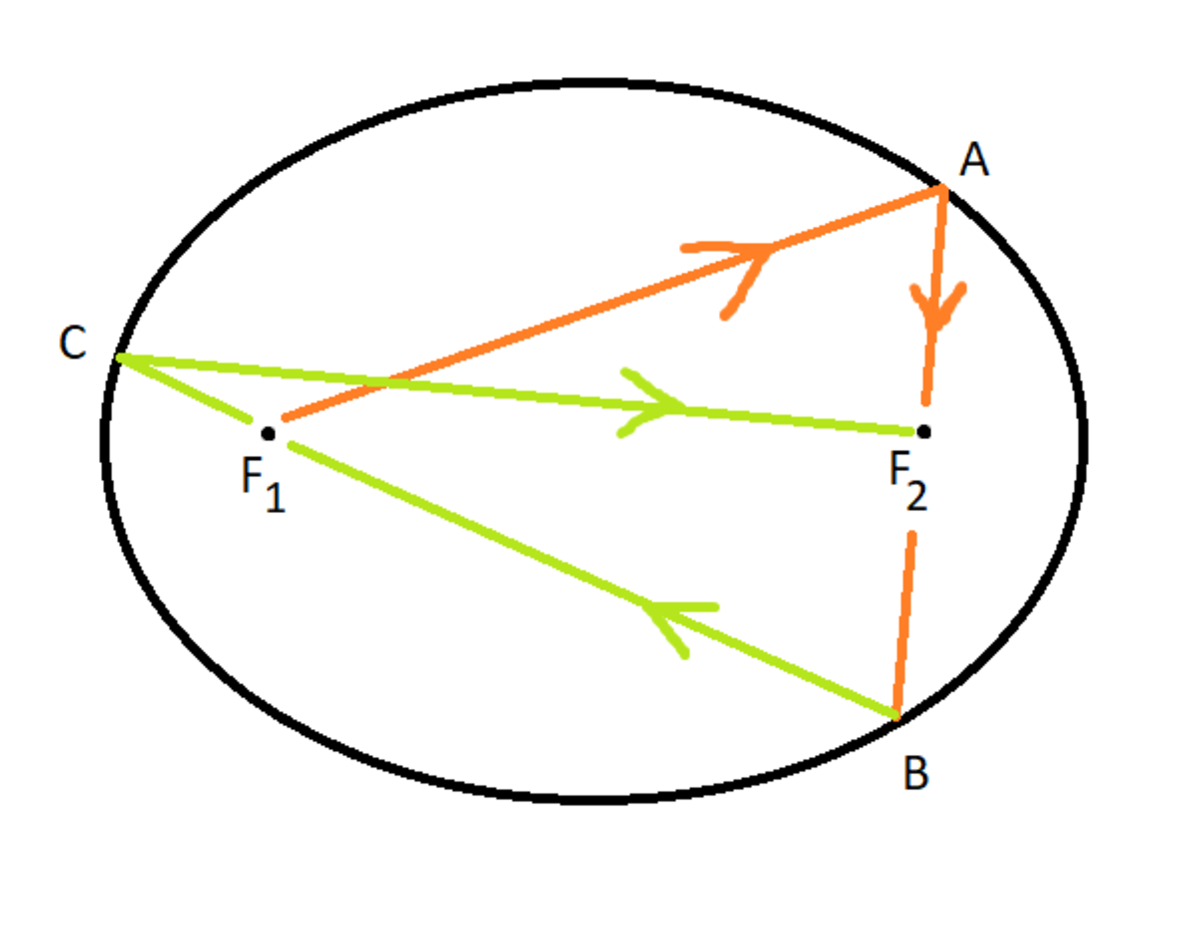
The ellipse shown above is given by

x 2 9 + y 2 4 = 1 \frac{x^2}{9} + \dfrac{y^2}{4} = 1

Its two foci are F 1 F_1 and F 2 F_2 . A ray of light (orange) starts from F 1 F_1 , gets reflected from the inner surface of the ellipse at point A A , then point B B , point C C , and finally reaches F 2 F_2 . Find the total length of its path. This is the sum of the lengths of the orange line segments and the green line segments.


The answer is 18.

Hosam Hajjir by Hosam Hajjir , 56, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

By definition of an ellipse, A F 1 + A F 2 = B F 1 + B F 2 = C F 1 + C F 2 = 2 a AF_1 + AF_2 = BF_1+BF_2 = CF_1 + CF_2 = 2a , where a = 3 a=3 is the major semi-axis. Therefore the total length of the line segments A F 1 + A F 2 + B F 1 + B F 2 + C F 1 + C F 2 = 6 a = 18 AF_1 + AF_2 + BF_1+BF_2 + CF_1 + CF_2 = 6a = \boxed{18}

3 Helpful 2 Interesting 2 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...