Regular Expressions
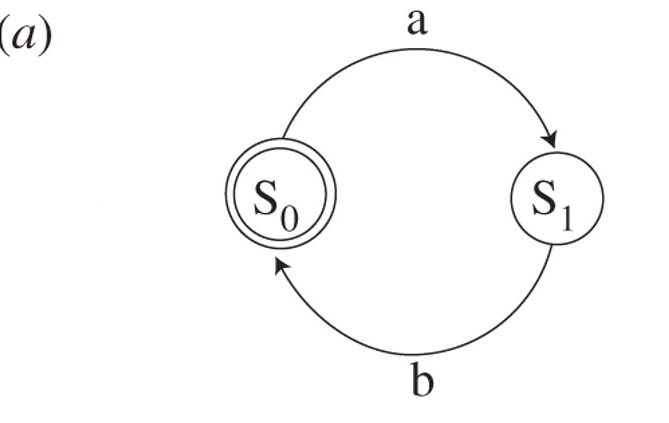
What regular expression is represented by the finite state machines shown below? is the starting state.
 http://rstb.royalsocietypublishing.org/content/367/1598/1933
http://rstb.royalsocietypublishing.org/content/367/1598/1933
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The answer is (ab)*. The starting state is S0, since the starting state is also the accept state, and there is no transition from the start state back into itself, the machine must transition from S0 to S1, which generates an "a". To get back to the accept state, we must transition, which adds a "b" to the string, yielding "ab" and this string can be repeated however many times because an "ab" cycle will start at the start/accept state and end there too.