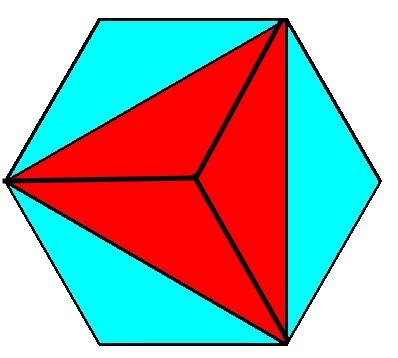
Regular hexagon

$Another solution:$

Let $x$ be the side length of the regular hexagon. Then the area of the three blue isosceles triangles is $A_{blue}=3\left(\dfrac{1}{2}\right)(x^2)(\sin 120)=\dfrac{3}{2}(x^2)\left(\dfrac{\sqrt{3}}{2}\right)=\dfrac{3}{4}x^2\sqrt{3}$ .

Now the area of a regular hexagon is given by $A_{hexagon}=\dfrac{3}{2}\sqrt{3}x^2$ .

So the area of the red region is

$A_{red}=A_{hexagon}-A_{blue}=\dfrac{3}{2}\sqrt{3} x^2-\dfrac{3}{4}\sqrt{3}x^2=\dfrac{3}{4}x^2\sqrt{3}$

Hence, the areas are equal.

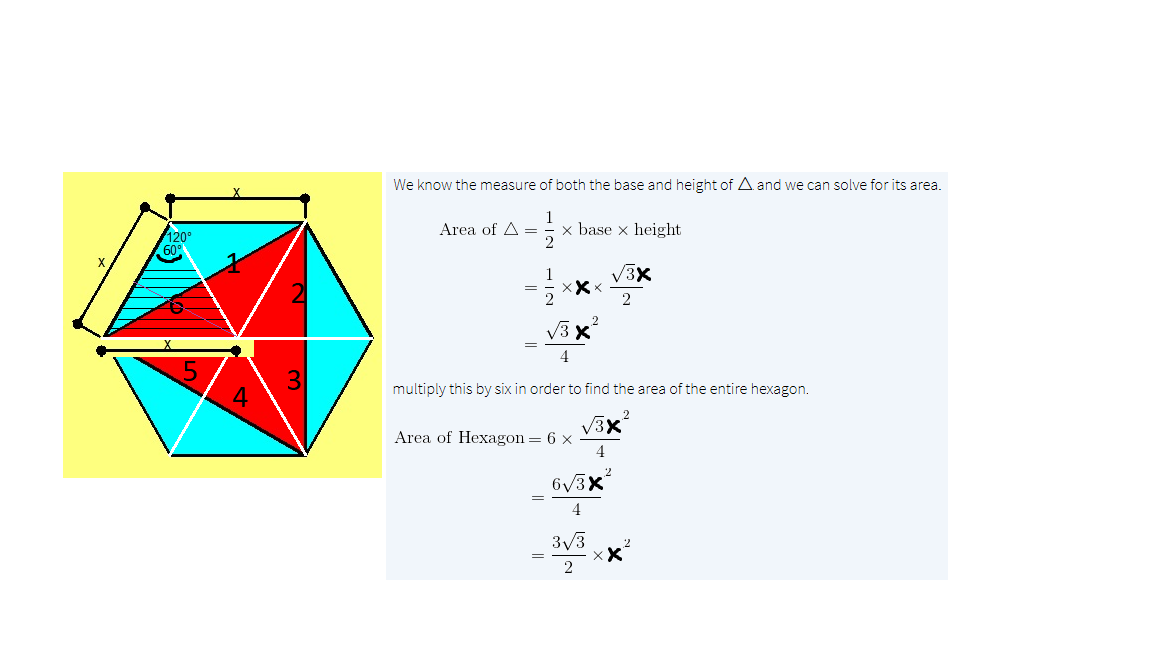
Draw lines equal in length to the lines creating the red triangle, and observe:

From this we find that the original lines divide the three parallelograms to create the hexagon in half, by bisecting the shapes. Because $1/2+1/2=1$ , we know that the two colored divisions are equal.

$A_{hexagon}=\dfrac{3}{2}\sqrt{3}x^2$

Now, length of side of red triangle = s = $\sqrt{3}{x}$ (twice the height of one of the six smaller equilateral triangles in diagram above)

Height of red triangle = h:
$\therefore\sqrt{{\left(\dfrac{\sqrt{3}{x}}{2}\right)}^{2}+{h^2}}=\sqrt{3}{x}$

$\therefore\dfrac{3x^2}{4}+{h^2}={3x^2}$

$\therefore{h^2} = {3x^2} - \dfrac{3x^2}{4}$ $\therefore{h^2} = \dfrac{9x^2}{4}$ $\therefore{h} = \dfrac{3x}{2}$

$A_{red} = \dfrac{s}{2}{h} = \dfrac{\sqrt{3}{x}}{2}\dfrac{{3x}}{2} = \dfrac{3}{4}\sqrt{3}x^2 = \dfrac{A_{hexagon}}{2}$

${A_{blue}} = A_{hexagon}-A_{red} = \dfrac{A_{hexagon}}{2}$ $\therefore{A_{red}} = A_{blue}$

Fold the blue triangles into the center. Since the hexagon angles are 120° and the triangle angles are 60°, they'll fit perfectly.

Let s be the side of the hexagon, and d be the chord joining every other vertex, The angle formed by adjacent hexagon sides, t = 4 180/6 = 120. The area of the blue part = 3 (1/2)s^2 sin(120) =[3 sqrt(3)/4] s^2. By the law of cosines, d^2 = s^2 + s^2 -2 s^2 cos(120) = 3s^2 The red area is an equilateral triangle with area = sqrt(3)/4 d^2 =[3 sqrt(3)/4] s^2, so they are equal. Ed Gray