Regular n-gon

Each internal angle of a regular $k$ -gon is $\frac{180^{\circ} \times \left(k-2\right)}{k}$ .

If there is a regular $n$ -gon obtained in the centre of the regular $k$ -gons, we have $\frac{180^{\circ} \times \left(n-2\right)}{n} = 360^{\circ} - 2\left(\frac{180^{\circ} \times \left(k-2\right)}{k}\right)$

Simplify it we have $1-\frac{2}{n}=\frac{4}{k}$

which is equivalent to $n=\frac{2k}{k-4} = 2+\frac{8}{k-4}$

This means that $k-4$ is a factor of 8. As $k\ge 5$ , $k-4=1,2,4$ or $8$ . So the sum of all possible value of $k$ is $16+15=\boxed{31}$ .

Despite $k \geq 5$ , we can also observe the cases for $k = 3$ and $k = 4$ . Let $\alpha$ and $\beta$ be the internal angles of regular $k$ -gon and $n$ -gon respectively. 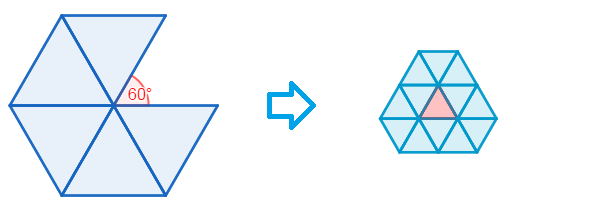Then: $\alpha = (1 - \dfrac{2}{k})180° \\ \beta = (1 - \dfrac{2}{n})180°$ What we are going to do is "glue" multiple regular $k$ -gons to form one angle of a regular $n$ -gon, and then use that patter $n$ times to form the regular $n$ -gon. For example, "gluing" $5$ equilateral triangles gives us a $60°$ angle, which can be used to form another equilateral triangle: Now let $x \in \mathbb{N}$ be the number of reuglar $k$ -gons glued. Obviously, $x > 1$ . $x$ angles of the $k$ -gon and an angle of an $n$ -gon will add up to $360°$ , as in the picture above: $\beta + x \alpha = 360°$ As $\beta$ is an angle of a regular polygon, it must satisfy: $60° \leq \beta \ < 180°$ So: $60° \leq \beta \ < 180° \\ 60° \leq 360° - x \alpha \ < 180° \\ -300° \leq - x \alpha \ < -180° \\ 180° < x \alpha \leq 300° \\ \boxed{\dfrac{180°}{\alpha} < x \leq \dfrac{300°}{\alpha}}$

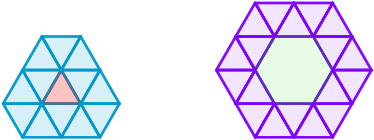
Now we determine $x$ for different values of $k$ . When $k = 3$ , we have $\alpha = 60°$ (equilateral triangle), so: $\dfrac{180°}{60°} < x \leq \dfrac{300°}{60°} \Rightarrow 3 < x \leq 5$ Which means that $x$ can either be $4$ or $5$ , implying $\beta = 120°$ or $\beta = 60°$ and $n = 6$ or $n = 3$ . In other words, this would mean that we can construct a regular hexagon or an equilateral triangle using only equilatreal triangles.

When $k = 4$ , we have $\alpha = 90°$ (square), and plugging this value for $\alpha$ in our inequality, we find $2 < x \leq \frac{10}{3}$ which implies that $x = 3$ and so $\beta = 360° - 3*90° = 90° \Rightarrow n = 4$ . This means that we can make a $90°$ degree angle using $3$ squares, and repeat the pattern $4$ times, to form another square in the center:

Now, for $k \geq 5$ , we have: $\alpha = (1 - \dfrac{2}{k})180° \geq (1 - \dfrac{2}{5})180° = 108° \\ x \leq \dfrac{300°}{\alpha} \leq \dfrac{300°}{108°} = \dfrac{25}{9} < 3$ Since $x > 1$ and $x < 3$ , it must be that $x = 2$ meaning that we can use only $2$ regular $k$ -gons to form an angle, which makes sense since for $k \geq 5$ , "gluing" more than $2$ $k$ -gons would result in $\beta < 60°$ or even $\beta < 0°$ where $k$ -gons would overlap. Now we solve the equation: $\beta = 360° - 2 \alpha \\ (1 - \dfrac{2}{n})180° = 360° - (1 - \dfrac{2}{k})360° \\ 1 - \dfrac{2}{n} = 2 - 2(1 - \dfrac{2}{k}) \\ 1 - \dfrac{2}{n} = \dfrac{4}{k} \\ \dfrac{2}{n} = 1 - \dfrac{4}{k} \\ n = \dfrac{2}{1- \dfrac{4}{k}} = \dfrac{2k}{k - 4} = \dfrac{2k + 8 - 8}{k - 4} \\ \boxed{n = 2 + \dfrac{8}{k - 4}}$ Now, $n$ and $k$ are both positive integers, so $k - 4$ must be a positive factor of $8$ , i.e. $(k - 4) \in \{1, 2, 4, 8\} \Rightarrow k \in \{5, 6, 8, 12\}$ Finally, solutions of this equation in ordered pairs for $k$ and $n$ are:

$(k, n) \in \{(5, 10), (6, 6), (8, 4), (12, 3) \}$

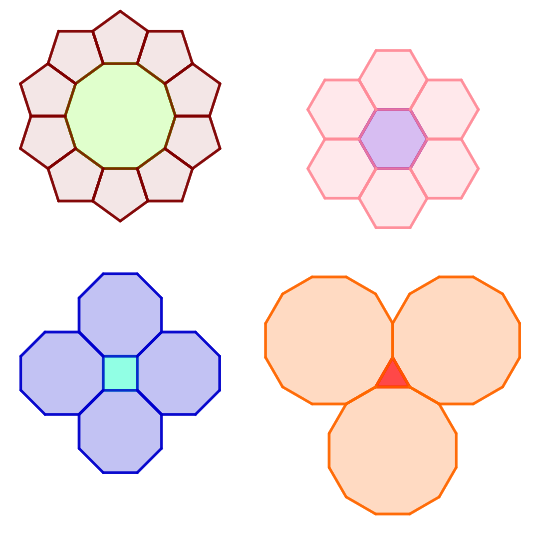
Or, in other words:

- $10$ regular pentagons make a regular decagon

- $6$ regular hexagons make another regular hexagon

- $4$ regular octagons make a square

- $3$ regular dodecagons make an equilateral triangle

The rule k=2n/(n-4) can be derived for creating a regular n-gons from placing k-gons together in a ring, which has possible integer solutions only with pairs (n,k)=(5,10), (6,6), (8,4) and (12,3). This sums to 5+6+8+12=31 for all possible n.

Answer=31

The sum of all the exterior angles of a polygon is 360 degrees. For an n-regular polygon, all exterior angles are going to be same; let's call it x. Then, x must be a factor of 360(since 360/x=n). Decagon's exterior angle x is 36 degrees. And as n must be greater than or equal to 10, x must be less than or equal to 36. Also, (x+180)/2 must be an internal angle of the k-regular polygon, which angle must satisfy (180)(k-2)/k, for an integer k. If you consider both conditions, only possible k greater than or equal to 5 are 5, 6, 8, and 12.