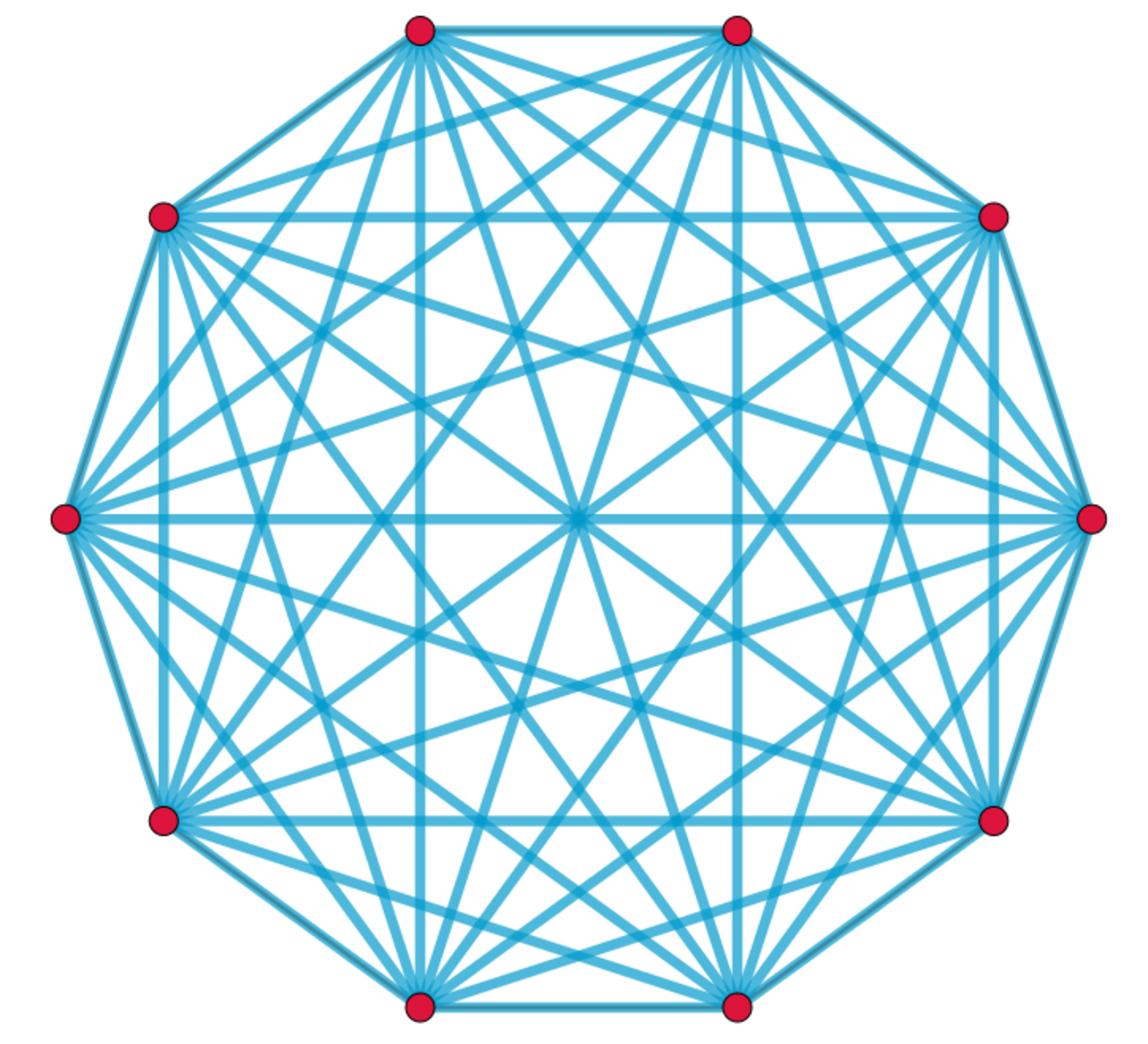
Regular polygon
There is exactly one cat sitting on each vertex of a regular decagon. Consider the polygon with all of its diagonals and sides. In every turn we choose a diagonal or a side, and the two cat, who are sitting on the two endpoints of the chosen line, change their places. After 45 turns, each side and diagonal was chosen exactly once. The cat or cats, who changed its/their places the most number of times, win(s).
If the winner cat(s) changed its/their places
number of times, then find the minimum value of
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Once you choose a diagonal/side, the cat on either end switches their place and has no way of going back to the same place it has been in before, as that line has been chosen already. Hence, the winning cat would have visited every single point, thus it would have switched places 9 times.