Regulating Power with Frequency
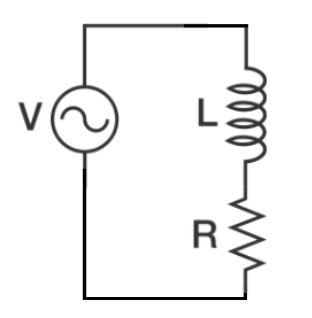
An ideal AC voltage source with frequency supplies a load consisting of a resistor and an inductor in series. At frequency , the load current lags the source voltage by 45 degrees, and the power (in Watts) dissipated by the load resistance is .
Suppose we want to decrease the power dissipated by the load resistance to by increasing the source frequency.
If this is accomplished by increasing the source frequency to a new value of , what is the value of ?
Note: Assume the resistance value to be constant
The answer is 1.732.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For the current to lag the voltage by 45 degrees, the resistance ( R ) and inductive reactance ( X ) must have the same magnitude at frequency f 0 . Find the power dissipated initially.
I = R 2 + X 2 V P = I 2 R = R 2 + X 2 V 2 R P R = R 0 2 + R 0 2 V 2 R 0
When the frequency is increased, the inductive reactance increases by the same ratio. The resistance retains its value (if we neglect the skin effect). Compare the new power to the old one.
R 0 2 + R 0 2 R 0 = 2 R 0 2 + X N 2 R 0 = 2 R 0 2 + α 2 R 0 2 R 0 R 0 2 + α 2 R 0 2 = 2 R 0 2 + 2 R 0 2 1 + α 2 = 4 α = 3
The new frequency is therefore 3 times the initial frequency.