Regulation Or Taxation?
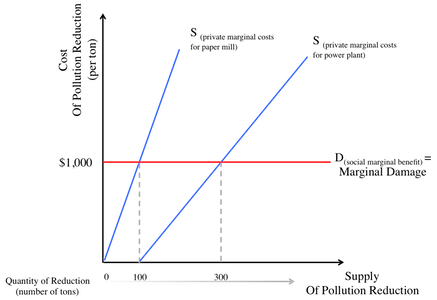
Suppose that there are two polluters in a city, both releasing C O X 2 into the atmosphere. One is a paper mill and the other is a power plant. The marginal damage from each ton of C O X 2 they produce is $ 1 , 0 0 0 , but they have different marginal costs to reduce that pollution, as represented by the graph to the right.
What's the most efficient solution for the government to reduce 400 tons of C O X 2 ? To establish a tax of $ 1 , 0 0 0 per ton of C O X 2 produced? Or to be fair, establish a policy that forces each plant to separately cut 200 tons of C O X 2 ? Assume that either taxation or regulation is enforceable and that an efficient solution means economically efficient.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Does the graph not show that the paper mill can eliminate 100 tons for $1000 and the power plant 300 tons for $1000. As the problem is written "tax of $1000 per ton". Would that not make the tax cost $400,000 to reduce 400 tons? So I would assume $2000 to reduce 400 tons is more efficient. Correct me if I'm wrong in the details written for this problem.
Log in to reply
Hello Justin - I've added some text to the graph itself to help clarify this. But the y-axis is cost/ton. So the paper mill can reduce 1 0 0 tons at a cost of $ 1 , 0 0 0 per ton = $ 1 0 0 , 0 0 0 , and the power plant can reduce 3 0 0 tons at a cost of $ 1 , 0 0 0 per ton = $ 3 0 0 , 0 0 0 under taxation. Under regulation, the paper mill would have to reduce 2 0 0 tons at a cost of $ 2 , 0 0 0 per ton (if it's a linear function with a slope of 1) + 2 0 0 tons from the power plant at the lower cost of $ 5 0 0 per ton = 2 0 0 × $ 2 , 0 0 0 + 2 0 0 × $ 5 0 0 = $ 5 0 0 , 0 0 0 from regulation.
At first, exegesis: Both polluters are probably releasing C O 2 continuously. Hence, I guess that 400 tons reduction per year is the aim. Then, what might be the C O 2 production per year in each plant? If it is far beyond 400 tons per year, the tax would probably motivate the paper mill to reduce 100 tons and the power plant to reduce 300 tons. Then both had still to pay tax, 1000 $ per ton of C O 2 . Summing up, both policies effectively reduce 400 tons, at no costs for the government. Both policies reduce marginal damage by 400000 $. The tax policy results in a transfer of money from polluters to government. Finally, government would have to invest this money into reafforestation of the Amazonas jungles in order to contribute to the fight against global warming.
So what is meant by 'efficient for the government'?
Thanks for commenting Jochem! The question asks for what is "most efficient", implying mathematical or economical efficiency (but I will update to make it clearer). It's just the government that's making the decision. Another way to look at this is, if the Marginal Costs for the paper mill is a linear function with points at ( 0 , $ 0 ) - it costs $0 to reduce 0 C O 2 pollution - and ( 1 0 0 , $ 1 , 0 0 0 ) then under a regulatory situation it would cost the paper mill $ 2 , 0 0 0 per ton to reduce 2 0 0 tons of C O 2 . For the Power Plant, assuming again a linear function from ( 1 0 0 , $ 0 ) to ( 3 0 0 , $ 1 , 0 0 0 ) , then it'd cost $ 5 0 0 per ton to reduce 2 0 0 tons of C O 2 . The total cost would be $ 2 , 0 0 0 × 2 0 0 + $ 5 0 0 × 2 0 0 = $ 5 0 0 , 0 0 0 . Versus a taxation situation where 4 0 0 tons can be reduced at a cost of $ 1 , 0 0 0 each = $ 4 0 0 , 0 0 0 . In this case taxation is cheaper than regulation for the parties involved.
I didn't even need to analyse the graph to solve this. I thought, well, if there was a request for both to cut off 200 tons of carbon dioxide, that would be pretty hard as you would need to consider the effects of this, ie. one polluter may not be able to do this, etc. As an analogy, you keep telling yourself to excercise but in reality, no 'threats' are there to constantly push yourself to achieve your goal, meaning you won't be able to do it.
Charging $1000 for a ton would reduce profits AND production for both, HOWEVER, it would serve as carbon tax and also effectively reduce carbon dioxide production as the $1000 regulation pressures the polluters to be decisive in what they produce and how they must produce it to minimise loss. Going back to the analogy, $1000 per ton is a threat and can cause some serious setbacks to the companies.
;) Roast me if I didn't properly answer the question.
Hello Rico - Generally in a supply and demand curve problem like this, where you're considering regulation, taxation, or another policy move, you assume that if the government makes a law that they'll be able to enforce that law. For instance, if the government passed a law that said each polluter must reduce C O 2 emissions by 2 0 0 tons that they'll be able to enforce that - through fines, police action, judicial procedures, etc. - so regulation has "threats" in the same way that taxation does. The government can affectively or directly shut the plant down. But, I'll add something in to make this clearer.
Also, there are situations where regulation is more affective. Just as a quick for instance, if you pretend that the pollution is nuclear leakage instead of C O 2 , in that case the marginal damage "curve" would change dramatically. It wouldn't be a flat horizontal line, but something approaching a flat vertical line. Any amount of nuclear leakage is very bad. In such a case, you wouldn't want one polluter to just reduce 1 0 0 tons of nuclear waste and then a tax for the next 1 0 0 tons. The deadweight loss would be huge. Instead, you'd regulate both to minimize nuclear leakage. Yes, this could mean that some polluter spends a tremendous amount of their capital to reduce the leakage, but this cost is outweighed by the social marginal damage caused by nuclear waste. All this is to say that the graph matters - the slope of the marginal damage curve is a big factor in whether a taxation or regulation or something else is the best policy.
Log in to reply
:) Thankyou for your comment, I shall learn from this.
The actual solution is to respect property rights. CO2 is not pollution (humans breathe it - plants need it), and taxation is theft.
Relevant wiki: Externalities
The most efficient solution is to provide a tax and let each polluter adjust according to their individual marginal costs. See the bottom of the wiki on Externalities for a way to make regulation work as well. But the main reason here, is that the paper mill can only reduce 1 0 0 tons of C O 2 for a cost at or below $ 1 , 0 0 0 per ton while the power plant can reduce 3 0 0 tons for that cost. The most efficient way to reduce total pollution by 4 0 0 tons is: for the paper mill to reduce 1 0 0 and the power plant to reduce 3 0 0 . This is achieved by a tax (and represented by the aggregate private marginal cost curve to the right). The regulation line shows that the paper mill would reduce C O 2 pollution at some high marginal cost, above $ 1 , 0 0 0 while the power plant was much lower, below $ 1 , 0 0 0 .