Relate between the orthocenter and $h_\text{max}$

Lemma: For an acute-angled triangle, $H$ lies within $ABC$ .

Proof: Read orthocenter .

Note: This implies that $AH, BH, CH > 0$ .

Lemma: Let the foot of the altitudes be $D, E, F$ . Then we have

$\frac{ AH}{AD} + \frac{ BH}{BE } + \frac{ CH}{CF} = 2$

Proof: Let the area of figure $PQRS$ be denoted by $[PQRS]$ .
Consider $\frac{ AH}{HD}$ . The ratio $\frac{ [ABH] } { [ABD ] } = \frac{ AH } { AD}$ as the triangles have the same height corresponding to the same base line. Similarly, $\frac{ [ACH]}{ [ACD] } = \frac{ AH } { AD }$ . Thus, we have $\frac{ [ABHC] } { [ABC ] } = \frac{ AH } { AD }$ .
We have similar equations for the other 2 fractions, which gives us

$\frac{ AH}{AD} + \frac{ BH}{BE } + \frac{ CH}{CF} = \frac{ [ABHC]} { [ABC] } + \frac{ [BCHA]} { [ABC] } + \frac{ [CAHB]}{[ABC]} = \frac{ 2 [ABC] } { [ABC] } = 2 . _\square$

Back to the question , since $AD, BE, CH \leq 4$ , hence we can conclude that

$\begin{array} { l l l } AH + BH + CH & = \frac{ AH }{ AD } \times AD + \frac{ BH}{BE } \times BE + \frac{ CH}{CF} \times CF \\ & \leq \frac{ AH}{AD} \times 4 + \frac{ BH}{BE } \times 4 + \frac{ CH}{CF} \times 4 \\ & = 2 \times 4 = 8 \end{array}$

Equality holds when $AD = BE = CF = 4$ , which occurs when we have an equialterial triangle.

---

As pointed out by Mark Henning, if we relax the constraints in the question to allow for right-triangles, then the above proof can be adapted in the following way.

1) Note that if $\angle A = 90^ \circ$ , then $H = A$ and so $AH = 0$ .
2) The proof of the geometry lemma still holds true. For right triangles, these fractions are either 0 or 1. However, for obtuse triangles, we have to use negative lengths to get this to work out.
3) For the inequality step, what we really want is the following:

Lemma: For $a_i, b_i \geq 0$ , define $S = \{ i | a_i = 0 \}$ . Then,
$\sum a_i b_i \leq \max_{ i \not \in S } b_i \times ( \sum a_i )$
with equality when $b_i$ is a constant for $i \not \in S$ .

4) Hence, in the equality case, we have to consider when the values of $AH, BH, CH$ are 0. For non-trivial triangles, at most one of them is 0, corresponding to the right-angled triangle. In this case, equality is achieved when the other altitudes are equal, meaning we have an isosceles right triangle.

The altitude $h_C$ from the vertex $C$ to the side $AB$ has length $h_C \,=\, b\sin A \,=\, 2R\sin A \sin B$ (where $R$ is the circumradius), with similar formulae for the other two altitudes $h_A,h_B$ . Thus, if we assume that the three angles $A,B,C$ in the acute-angled triangle are such that the angle $A$ is the smallest, so that $0 \le A \le B,C \le \tfrac12\pi$ , then the longest altitude is $h_\mathrm{max} \,=\, h_A \,=\, 2R\sin B \sin C$ . Thus we must assume that $0 \le A \le B,C \le \tfrac12\pi$ , and that $R\sin B \sin C = 2$ .

It is well known that, for an acute-angled triangle, the length $AH$ is twice the distance from the circumcentre to the side $BC$ , so that $AH \,=\, 2R\cos A$ . Simlarly $BH \,=\, 2R\cos B$ and $CH \,=\, 2R\cos C$ , and hence $\begin{array}{rcl} AH + BH + CH & = & \displaystyle 2R(\cos A + \cos B + \cos C) \; = \; 4\frac{\cos A + \cos B + \cos C}{\sin B \sin C} \\ & = & \displaystyle 4 \frac{\cos B + \cos C - \cos(B+C)}{\sin B \sin C} \; = \; 4 + 4 \frac{\cos B + \cos C - \cos B \cos C}{\sin B \sin C} \\ & = & 4 + 4\big(\cot B \mathrm{cosec}\,C + \mathrm{cosec}\,B \cot C - \cot B \cot C\big) \; = \; 4 + 4F(B,C) \end{array}$ 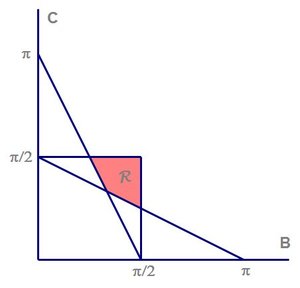Thus we want to maximize $F(B,C)$ over the relevant range of values of $B,C$ . Since $A+B+C = \pi$ and $0 \le A \le B,C \le \tfrac12\pi$ , we deduce that $\pi - B - C \le B,C$ , and hence it follows that $B,C$ must lie in the region $\mathcal{R}$ defined by the inequalities $2B + C \ge \pi \hspace{1cm} B + 2C \ge \pi \hspace{1cm} B \le \tfrac12\pi \hspace{1cm} C \le \tfrac12\pi$ Thus $\mathcal{R}$ is the quadrilateral region defined by the vertices $(\tfrac12\pi,\tfrac14\pi)$ , $(\tfrac12\pi,\tfrac12\pi)$ , $(\tfrac14\pi,\tfrac12\pi)$ and $(\tfrac13\pi,\tfrac13\pi)$ . Since $\begin{array}{rcl} \displaystyle \frac{\partial F}{\partial B} & = & \displaystyle -\mathrm{cosec}^2B \mathrm{cosec}\,C\big[1 + \cos B \cos C - \cos C\big] \\ \displaystyle \frac{\partial F}{\partial C} & = & \displaystyle -\mathrm{cosec}\,B \mathrm{cosec}^2C\big[1 + \cos B \cos C - \cos B\big] \end{array}$ we see that $\nabla F \,=\, 0$ only when $1 + \cos B \cos C \,=\, \cos B \,=\, \cos C$ . Since the quadratic equation $1 + t^2 = t$ has no real roots, we deduce that there are no points where $\nabla F = 0$ . The the maximum value of $F$ over the region $\mathcal{R}$ must be achieved on the boundary of $\mathcal{R}$ . Since $F$ is a function that is symmetric in $B$ and $C$ , we only need check the behaviour on half the boundary.

• It is clear that $F(B,\tfrac12\pi) = \cot B$ is a decreasing function of $B$ for $\tfrac14\pi \le B \le \tfrac12\pi$ , and so $F(B,\tfrac12\pi) \le 1$ for $\tfrac14\pi \le B \le \tfrac12\pi$ .
• We note that $F(B,\pi-2B) \; = \; \cot B \mathrm{cosec}\,2B - \mathrm{cosec}\,B \cot2B + \cot B \cot 2B \; = \; \frac{2\cos^3 B - \cos 2B}{2\sin^2B \cos B}$ so that $1 - F(B,\pi - 2B) \; =\; \frac{2\sin^2B \cos B - 2\cos^3B + \cos 2B}{2\sin^2B \cos B} \; =\; \frac{\cos2B(1 - 2\cos B)}{2\sin^2B\cos B}$ If $\tfrac14\pi \le B \le \tfrac13\pi$ , then $\cos2B \le 0$ and $\cos B \ge \tfrac12$ , which means that $F(B,\pi - 2B) \,\le \, 1$

We deduce that the maximum value of $F(B,C)$ over the region $\mathcal{R}$ is $1$ , and this is achieved at the points $(\tfrac12\pi,\tfrac14\pi)$ , $(\tfrac14\pi,\tfrac12\pi)$ and $(\tfrac13\pi,\tfrac13\pi)$ .

Thus the maximum value of $AH + BH + CH$ , subject to the condition $h_\mathrm{max} = 4$ , is $\boxed{8}$ . This maximum value is achieved either by an equilateral triangle or by an isosceles right-angled triangle.

In $\Delta ABC$ let $D$ and $E$ be the feet of altitudes on $AB , BC$ from vertices $C , A$ respectively and $AE$ be the maximum altitude. $\Rightarrow AB , AC \ge BC.$ Also, let $\angle B \ge \angle C.$

Our Claim $- 2AE \ge AH + BH + CH.$

Proof $- 2 AE \ge AE + CD$ . So, it suffices to prove that $AF + CD \ge AH + BH + CH \Rightarrow HE + HD \ge BH$

Applying Ptolemy's theorem in cyclic qua. $BDHE$ ,

$BE \times HD + BD \times HE = BH \times DE$

But $\angle C \ge \angle A \Rightarrow \angle EBH \le \angle DBH \Rightarrow BE \ge BD$ Using in above equation:

$\Rightarrow BE \times (HE + HD) \ge BH \times DE$ $-1$

But, $\Delta BDE \sim \Delta BCA \Rightarrow \angle BDE = \angle C \Rightarrow \angle B \ge \angle BDE$

$\Rightarrow DE \ge BE$ $- 2$

Thus from $1 , 2$ $\Rightarrow HE + HD \ge AH.$ Thus $2 AE \ge AH + BH + CH$ So, the $AH + BH + CH$ achieves its maximum value at 8.

An another question guarateeing the uncertainty of INMO problems. :)

this solution is not correct, BUT a JEE style. since the $\triangle ABC$ is given acute and no other condition given for triangle, I considered the triangle ABC to be equilateral and then perpendiculars and centroid are in same line .

$\begin{aligned} AH= \frac{8}3 = BH = CH\\ max (AH+BH+CH) = \boxed 8 \end{aligned}$

Again i have not proved triangle to be equilateral but I just let the h max to be equal and possible in the case of Equilateral triangle, Hope it helps :D . For more clarification please see @Mark hennings solution.