Related Rates

Calculus Level 3

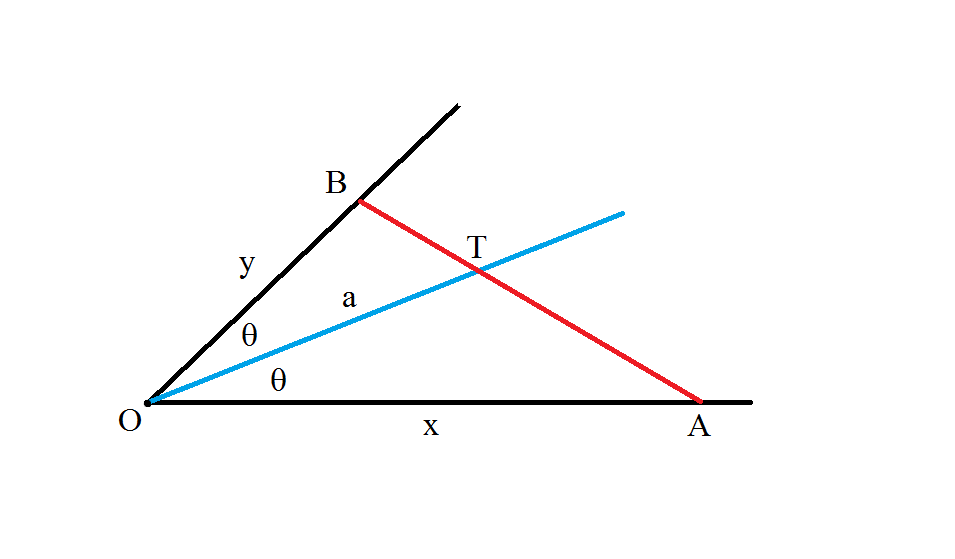
Two lines intersect at $O$ making an angle of $2 \theta$ between them, where $\theta =30^{\circ}$ . $T$ is a point on their angle bisector that is $a = 5$ units away from $O$ . Point $A$ is on one line and point $B$ is on the other line such that $A$ , $T$ and $B$ are collinear.

If point $A$ is moving with constant speed of 1 unit per second towards point $O$ . How fast is point $B$ moving away from point $O$ , at the instant when $x = | OA | = 5$ ?

Give your answer to 3 decimal places.

The answer is 1.866.

2 solutions

Hosam Hajjir
Sep 3, 2016

Let $\phi = \angle OTB$ , then using the law of sines in triangles $OTB$ and $OTA$ , we obtain,

$\dfrac{\sin( \phi - \theta ) }{a} = \dfrac{\sin( \phi ) }{x}$

and

$\dfrac{\sin( \phi + \theta ) }{a} = \dfrac{ \sin( \phi ) } {y}$

Adding the two equations, and simplifying, we get

$\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{ 2 \cos \theta }{a} \cdots (1)$

Differentiating w.r.t. time,

$- \dfrac{1}{x^2} \dfrac{dx}{dt} - \dfrac{1}{y^2} \dfrac{dy}{dt} = 0$

From which,

$\dfrac{dy}{dt} = - \left( \dfrac{y}{x} \right)^2 \dfrac{dx}{dt} \cdots (2)$

Usiing (1) we can find $y$ and substitute it in (2) , to obtain

$\dfrac{dy}{dt} = \boxed{1.866}$

@Hosam Hajjir Calculus works of course, but if we consider the geometry and motion too, it becomes much simpler.

Velocities

Let Ra, Rb = velocities of points A and B, due to the rotation of AB about T. But this will take them off the lines OA and OB, so they must slide back on with velocities Sa, Sb, perpendicular to Ra, Rb. This results in the effective velocity Va = 1, giving Ra = cos 15°. Rb will be in the same direction but in opposite sense and in the ratio TB/TA. It along with Sb would give required velocity Vb as follows.

The velocity triangle at A is 15°-75°-90°, that at B is 45°-45°-90°

$Ra \times \frac{TB}{TA} \sqrt{2} = \cos 15° \frac{5/\sqrt{2}}{10 \sin 15°} \sqrt{2} = \frac{1}{2 \tan 15°}= 1.8660254$

Hi @Brian Charlesworth Thought you might like this :-)

Ujjwal Rane - 4 years, 9 months ago

This solution is very insightful. Thanks for sharing it.

Hosam Hajjir - 4 years, 9 months ago

Thanks @Hosam Hajjir :-) motion has tremendous potential of simplifying certain problems, some of which may not even involve motion explicitly.

BTW, I thought of shifting it as a separate solution. So I will replace the comment with a pointer like 'see the solution posted'. Hope that is ok.