Related to Open Problem #1: In the Corner
On a chessboard of a finite size, we want to place kings and knights such that each king attacks exactly 2 kings and 2 knights and each knight attacks exactly 2 kings and 2 knights.
What can we say about the square adjacent to a corner (horizontally or vertically, not diagonally)?
The possible attacks of a knight are shown on the left, and the possible attacks of a king are shown on the right.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Every knight must attack at least 4 squares to attack 2 kings, and 2 knight, so the square isn’t allowed to have a knight.
To figure out if a king may go in the square, assume it does and extrapolate that decision until either a complete board is created that satisfies the conditions, or a contradiction is detected.
The king attacks 5 squares, and exactly 2 of those squares must be knights and 2 must be kings.
Square a8 isn’t allowed to have a king, because it would then attack only 3 squares. It’s also not allowed to have a knight, because it would attack only 2 squares. Therefore a8 has to be empty.
Square b8 isn’t allowed to have a knight for the same reason a7 wasn’t allowed to have a knight, so it has to have a king. We now have the following setup (I use black pawns to visualize which squares have to be empty):
We now need to place 1 more king and 2 knight in the squares b7, a6, and b6. There are three ways to do that.
1: Place the king on b7
This formation isn’t possible. The king on b7 already attacks 2 kings and 2 knights. Therefore c7 has to be empty. However, the knight on a6 attacks only 4 squares, including c7, which means c7 is not allowed to be empty.
2: Place the king on b6
This formation also isn’t possible. The knight on a6 attacks 4 squares, including c7 and c5, so both squares need to have a piece. However, the king on b6 already attacks 3 pieces, so at least 1 of the squares c7 and c5 has to be empty.
3: Place the king on a6
The king on b8 has to attack one more king, and one more knight. Using the same logic we used at #2: Place the king on b6, we can deduce that the king has to go on c8, and the knight on c7.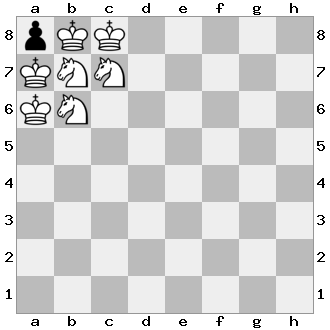
The knight on b7 attacks only 4 squares, so a5, c5, d6, and d8 all must have some piece (I use white pawns to visualize squares that must have either a king or a knight, but it’s not yet clear which of the two it is).
The king on a6 already attacks 1 king and 2 knights, so a5 has to be a king, and b5 has to be empty. Similar logic is used to determine d8 must have a king, and d7 has to be empty. The knight on b7 now attacks 2 kings, so the remaining 2 squares it attacks should both be knights.
The kings on a5 and d8 already attack 1 king, 1 knight, and 1 empty square, so a4, b4, e8, and e7 must all have some piece. The knight on b6 attacks 1 king, 1 empty square, and 3 other squares, so d5 and c4 have to have some piece as well. Similar logic with the knight on c7 can get used to prove e6 must have some piece.
The knights on c5 and d6 now attack 4 pieces, so the squares f7, f5, e4, d3, and b3 have to be empty.
The squares a4, and e8 can no longer be kings, because those would attack only 3 squares. Therefore a4, and e8 have to be knights, and b4, and e7 have to be kings.
The kings on b4 and e7 now attack 1 king, 2 knights, and 1 unknown piece, so the squares c4, and e6 have to be kings, and the squares a3, c3, f6, and f8 have to be empty.
We’ve now reached a contradiction. The knight on a4 attacks only 4 squares, so c3 has to have some piece. However, that square is currently empty. Therefore our initial assumption that a king on a7 was a valid start was false.
Since a knight is not allowed to go on a7, and placing a king on a7 will result in a contradiction, the square next to the corner has to be empty. Therefore the correct answer is 'The square can neither have a knight, nor a king'.