Related to Open Problem #1: Knights and Knights
This problem is part of the new Brilliant.org Open Problems Group . The end goal for each open problem is to find a solution, and maybe publish it if it's a nice enough result! Even if we don't make it all the way there, we can have fun exploring unsolved problems and doing real research. This problem is related to an unsolved open problem, which you can read about here .
Place an equal number of white knights and black knights on a square board (of any size) such that
- each white knight is attacking 2 other white knights and 2 black knights;
- each black knight is attacking 2 other black knights and 2 white knights.
What is the side length of the smallest square board on which this is possible?
Note: A chess knight moves in an "L" shape either 1 square vertically and 2 squares horizontally or 2 squares vertically and 1 square horizontally, as indicated by the stars above.
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Moderator note:
Just a quick reminder to those reading this far: this is part of the Brilliant.org Open Problems group . We've already found some interesting results and made a wiki for gathering data . Come join us!
Any other possible solutions?
I think you can swap white knights with black knights in middle row or middle column and the solution is still valid.
1. Is this the only configuration?
2. Is this the only configuration if we're trying to minimize the board size?
3. How many ways are there of doing this?
So I think it's well-proven that the minimal board size is 7 × 7 .
However, some questions arise to our brilliant minds. Then how about we go deeper?
1. Is this the only configuration?
No. There are other ways.
One way is to just simply copy the configuration and then paste it on a pretty distant place.
2. Is this the only configuration if we're trying to minimize the board size?
Yes, you plug in the colors in the below diagram.
It is found by trying to minimize the whole size with one type of knights. (since one knight must threaten exactly 4 other knights)
and thus this is the only-smallest configuration.
3. How many ways are there of doing this?
If we consider rotating/flipping as another way of making the diagram, then there are 3 8 4 ways of doing this.
Lemme explain.
First, pick any point from the diagram. [there are 1 6 ways of doing this.]
Next, pick any point that is connected by a line and eliminate all other points that were the option. [there are 4 ways of doing this.]
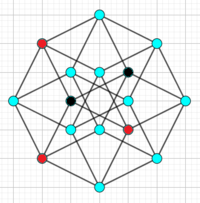
Then do it again. [there are 3 ways of doing this.]
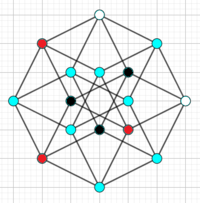
Again! [there are 2 ways of doing this.]
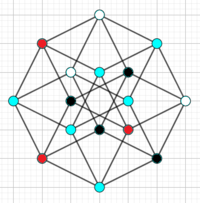
Again... [there are 2 ways of doing this.]
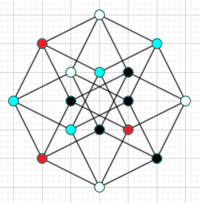
Again...? [there are 2 ways of doing this.]
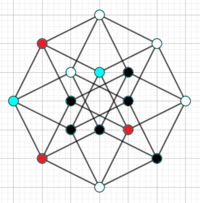
...again. [there are 2 ways of doing this.]
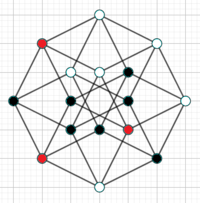
After that, revive all the red points, and then select from the two options that you've got. [there are 2 ways of doing this.]
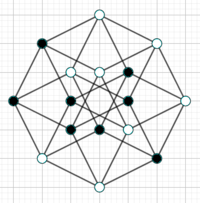
Then you'll realize you've made a c l o s e d p a t h !
The rest of the places are, as you may have assumed, for white knights to occupy. :P
Therefore the number of cases is 1 6 × 4 × 3 × 2 × 2 × 2 × 2 × 2 = 6 1 4 4 .
Wait, no. This is a c l o s e d p a t h with length 8 .
So we must divide that number by 1 6 , to avoid duplicates.
Hence the number of cases is 6 1 4 4 ÷ 1 6 = 3 8 4 .
You should consider joining us at the Open Problems Group to work on the unsolved problem that looks like this. We also now have a wiki page dedicated to gathering information about it .
Shouldn't you divide by 2 one more time, since you are counting directed paths, and we are only interested in non-directed patterns?
Log in to reply
Ah, right, sorry. Didn't think about that. Thanks for pointing out!
Thanks for that. I can publish a research paper now!
| _ | _ | _ | B | _ | _ | _ |
| _ | B | _ | _ | _ | W | _ |
| _ | _ | B | B | W | _ | _ |
| W | _ | W | _ | W | _ | W |
| _ | _ | W | B | B | _ | _ |
| _ | W | _ | _ | _ | B | _ |
| _ | _ | _ | B | _ | _ | _ |
I guest 7 and it was right the first try.
It wasn't really a solution. I just looked at it then guessed 7, although I mentally did extrapolate the coverage of a board with two knights 'at full reach' which clearly requires a minimum of seven squares.
The right-hand diagram shows that it is possible to do this with a 7 × 7 square.
If we tried to place the knights on a 6 × 6 board, then (every knight has to attack four squares) no knight can go on the corner squares or the eight squares adjacent to the corners. Although the other edge squares attack four squares, they cannot be used either, since they attack the squares adjacent to the corners, and so a knight there would have to attack another knight that could only attack at most three other knights. Thus no knight can go on the edge, and so we are in fact forced to try to achieve the arrangement of knights on a 4 × 4 board.
If we tried to place the knights on a 5 × 5 board, then (for exactly the same reasons as above) we could not place a knight on any edge square, and so we would be attempting a knight arrangement on a 3 × 3 board.
If we tried to place the knights on a 4 × 4 board, then (again) we could not use any of the edge squares, so would be restricted to a 2 × 2 board.
No knight on a 3 × 3 board or smaller can attack four other knights.
Thus the size of the smallest possible square board for which this arrangement of knights is possible is 7 × 7 .