Relationship between medians
There is a triangle A B C such that A C 2 = A B 2 + B C 2 . Two of its medians are of length 5 and 7 . Find the sum of the square of possible lengths of third median.
The answer is 90.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
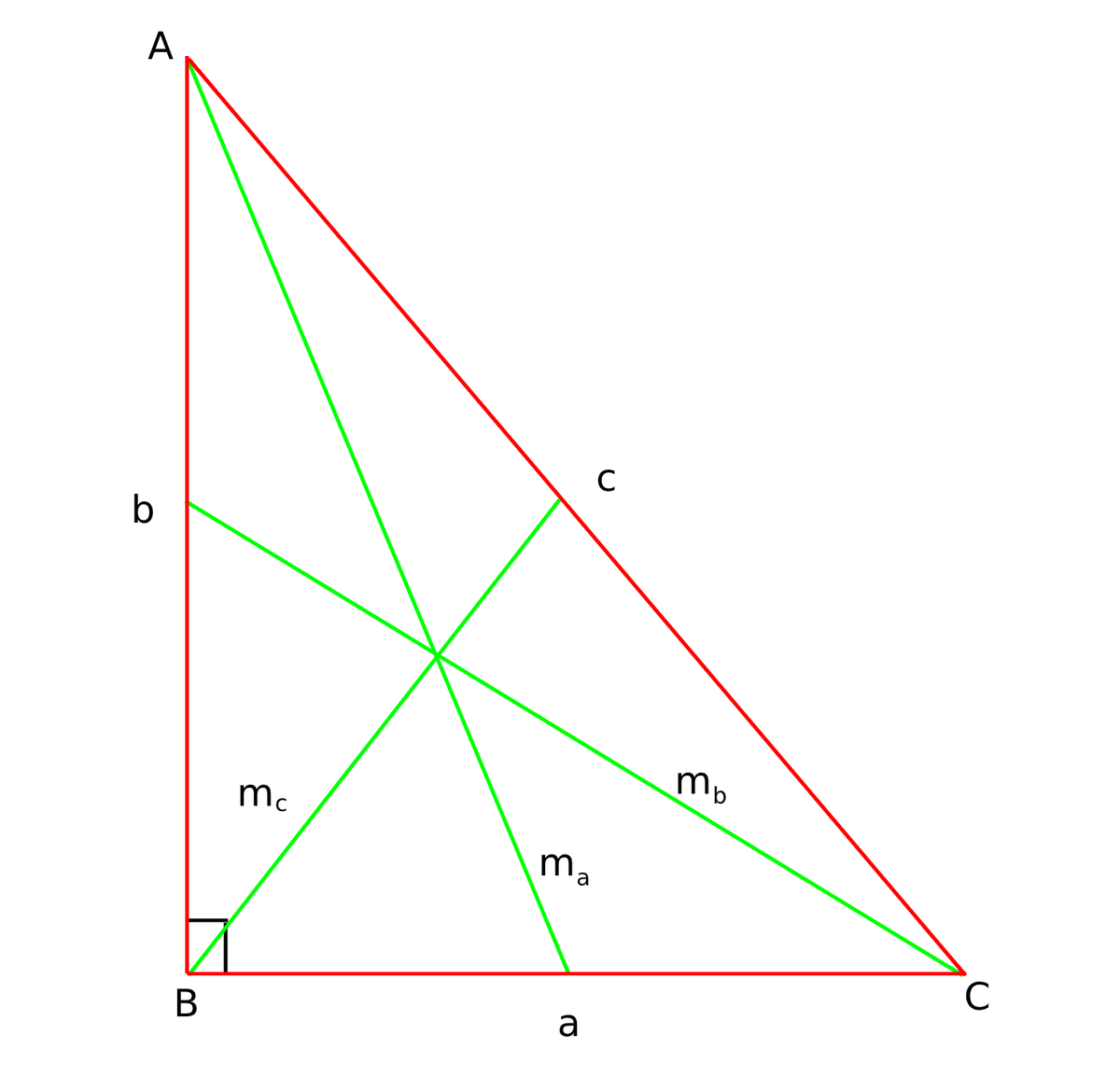 Since
A
C
2
=
A
B
2
+
B
C
2
,
△
A
B
C
is a right triangle right angled at
B
by converse of pythagoras theorem.
Since
A
C
2
=
A
B
2
+
B
C
2
,
△
A
B
C
is a right triangle right angled at
B
by converse of pythagoras theorem.
Let B C = a , A B = b , A C = c , m a , m b and m c are the lengths of medians on B C , A B and A C .
From pythagoras theorem,
m a 2 = b 2 + 4 a 2
m b 2 = a 2 + 4 b 2 and
m c 2 = 4 c 2 = 4 a 2 + b 2 [Twice of median on hypotenuse of right triangle equals to hypotenuse]
Eliminating a and b from the above equations we get,
m a 2 + m b 2 = 5 m c 2 ⋯ Eq. 1
Also, when m a , m b and m c are given, a , b and c can be find out using above 3 equations as:
c 2 = 4 m c 2
b 2 = 1 5 4 ( 4 m a 2 − m b 2 ) and
a 2 = 1 5 4 ( 4 m b 2 − m a 2 )
Since a , b and c are greater zero. Constraints on m a , m b and m c are as :
2 m a > m b and 2 m b > m a
Using these constraints in Eq. 1 we will get
m a > m c and m b > m c
Now coming to our question, based on these 4 constraints there are 4 possible cases:
- m a = 5 , m b = 7 , m c to be determine.
- m b = 5 , m a = 7 , m c to be determine.
- m b = 7 , m c = 5 , m a to be determine.
- m a = 7 , m c = 5 , m b to be determine.
Using Eq. 1 , we can get the length of third median. From the first two cases,
m c 2 = 5 m a 2 + m b 2 = 5 5 2 + 7 2 = 5 7 4
From case 3,
m a 2 = 5 m c 2 − m b 2 = 5 ⋅ 5 2 − 4 9 = 7 6
From case 4,
m b 2 = 5 m c 2 − m a 2 = 5 ⋅ 5 2 − 4 9 = 7 6
So, square of possible lengths of third median are 5 7 4 and 7 6 . Hence their sum is 5 7 4 + 7 6 = 5 4 5 4 = 9 0 . 8
Let the position coordinates of A , B , C be ( 0 , c ) , ( 0 , 0 ) , ( a , 0 ) respectively. Then we have two sets of equations :
(i) 4 a 2 + c 2 = 2 5
a 2 + 4 c 2 = 4 9
We have to find the value of 4 a 2 + c 2 , which is 5 7 4 = 1 4 . 8 .
(ii) 4 a 2 + c 2 = 2 5
a 2 + 4 c 2 = 4 9
We have to find the value of 4 a 2 + c 2 , which is 7 6 .
Hence the sum of these two values is 1 4 . 8 + 7 6 = 9 0 . 8 .