Relative motion
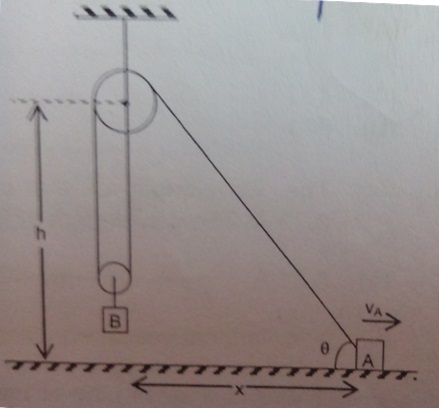 If block
A
is moving horizontally with velocity
v
A
, then find the velocity of block
B
at the instant as shown.
If block
A
is moving horizontally with velocity
v
A
, then find the velocity of block
B
at the instant as shown.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice can u post something for this
Nice solution. Yours is a BETTER and engineering method. I have given below the problem from point of view of calculus.
T a n θ = x h , a n d S i n θ = R h , w h e r e R 2 = h 2 + x 2 . ⟹ h = x ∗ T a n θ , a n d h = R ∗ S i n θ . C o s θ = x 2 + h 2 x D i f f e r a n t i a t i n g w . r . t . t i m e a n d e q u a t i n g d t d θ f r o m b o t h , x ∗ s e c 2 θ V A ∗ T a n θ = R ∗ C o s θ . V R ∗ S i n θ ∴ V R = x ∗ s e c 2 θ V A ∗ T a n θ ∗ S i n θ R ∗ C o s θ . B u t V B = 2 1 ∗ V R = 2 1 ∗ V A ∗ x 2 + h 2 x .
On second thought:-
A s is the endpoint of the string that is connected to block A. ∴ V A S i s a c o m p o n e n t o f V A . ⟹ V A S = V A ∗ C o s θ = x 2 + h 2 V A ∗ x . Free points on the string to the right of pulley and the right tangency point ON the pulley at B have velocity of V A S . Similarly, on the left , and left tangency point ON the pulley has 0 velocity(are stationary). So, the midpoint between the points of tangency ON the RIGID pulley, where the block B is attached has velocity V B = 2 V A S = 2 ∗ x 2 + h 2 V A ∗ x .
Let's invoke the Virtual Work done method!!
This method states that the work done by the internal forces in case of a mechanical system is always zero. In this case, the internal forces are the tension in the strings. Let string attached with block ′ A ′ has a tension ′ T ′ in it. Clearly, the string attached to block ′ B ′ has tension ′ 2 T ′ in it.
Now, the velocity component of ′ A ′ in the direction of tension is v A cos θ . So, by virtual work done:
T A x A + T B x B = 0
Differentiating this equation with respect to time, we can get that:
T A v A + T B v B = 0 T v A cos θ + 2 T v B = 0
From the adjacent triangle,
cos θ = h y p o t e n u s e b a s e = x 2 + h 2 x
Using this information, and ignoring the negative sign, which gives direction, we get:
v B = 2 T T v A cos θ = 2 x 2 + h 2 x v A
CHEERS!!:)