Relative Scale for a truncated dodecahedron
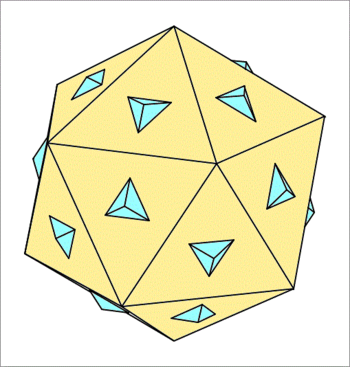
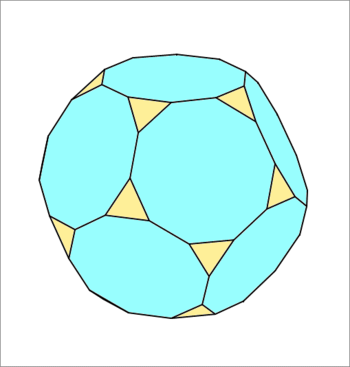
The above figure depicts the intersection of a dodecahedron (blue) with an icosahedron (yellow) whose edge length is times the edge length of the dodecahedron, such that the resulting polyhedron of intersection is the one shown below having regular 10-sided decagons (blue) and equilateral triangles (yellow) all with the same edge length. Find the relative scale factor (the ratio of the edge length of the icosahedron to the edge length of the dodecahedron). As your answer enter .
The answer is 17236.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The shape I'm going to use to relate the two lengths together is that 5-sided Diamond one, where one of the upper diagram's little tetrahedron's longer side (which borders the original polyhedra intersection) becomes the upper horizontal side, 2 shorter sides from that tetrahedron's vertices and perpendicular to the nearest icosahedron's sides and the last are 2 half sides of the icosahedron's equilateral triangle's that meet at the lowest point at 60°.
If we let the little tetrahedron's shorter (climbing) side have a length of 2, our dodecahedron will have a side of 2 + (1 + √5) + 2 = 5 + √5.
As for the icosahedral pentagonal pyramid, if the side length is 4, then the base longest diagonal would be 2 + 2√5. Thus the ratio of the diamond's shortest side to half the final octagonal side equals 2√3 : 1 + √5. From our earlier supposition of octagonal side = 1 + √5, then the diamond's shortest side = √3. This length is perpendicular to icosahedral side, so if we divide the diamond into upper trapezoidal shape and lower equilateral triangle with a third half side, it would make a 90° - 60° = 30° with that √3 side. Therefore, our icosahedral half side = 2 × (√3 / 2) × √3 + (1 + √5) = 4 + √5, so the full length would be twice that with 8 + 2√5.
Answer
= floor[10000 × (8 + 2√5) / (5 + √5)]
= floor[500 × (8 + 2√5) × (5 - √5)]
= floor[500 × (30 + 2√5)]
= 15000 + floor[1000√5)]
= 17236