Relatively hard. Won't you say?
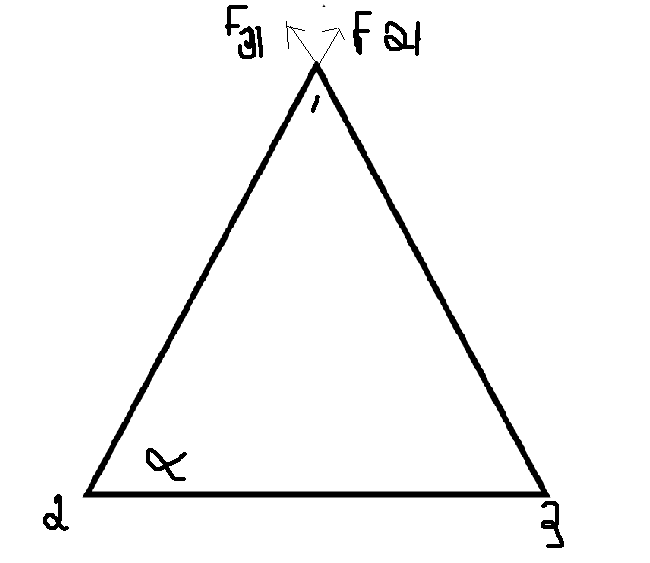 Calculate the force on charge 1 (find sum the total x and y forces.Given
α
=
6
0
,charge 1,2,3 have
+
1
1
×
1
0
−
6
coulombs of charge, and finally the distance between the charges is
.
1
5
m
Calculate the force on charge 1 (find sum the total x and y forces.Given
α
=
6
0
,charge 1,2,3 have
+
1
1
×
1
0
−
6
coulombs of charge, and finally the distance between the charges is
.
1
5
m
The answer is 83.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
First we need our basic formulas F = d 2 K × q × q .Thus we have the equation lets calculate the force as follows F 2 1 = F 3 1 . 1 5 2 9 ∗ 1 0 9 × + 1 1 × 1 0 − 6 = 4 8 . 4 N . Now let us calculate the x , it is obvius that we are going to get F t o t a l x o f F 2 1 = f o r c e × c o s α = 4 8 . 4 ∗ c o s ( 6 0 ) = 2 4 . 2 and these the other f 2 1 =-24.2 so they cancel each other.Now we need the y forces acting in two directions first F t o t a l x i n 2 1 = f o r c e × c o s α = 4 8 . 4 ∗ s i n ( 6 0 ) = 4 1 . 9 and the the other y dirction F t o t a l x i n 3 1 = f o r c e × c o s α = 4 8 . 4 ∗ s i n ( 6 0 ) = 4 1 . 9 so the sum of those forces gives you 8 3 . 8 . Sorry explanation in picture would be more helpful but i don't know how to display picture
Since the distance between each charge is the same, they must be on the vertices of an equilateral triangle. Therefore, the x-components of the electrostatic force cancel out, and the y-components of the forces from 2 and 3 will be the same (since they have the same charge).
Each y-component force will be F sin α where F = magnitude of the force. Hence:
Σ F = 2 sin α × r 2 k Q 1 Q 2 = 2 sin 6 0 o × 0 . 1 5 2 ( 8 . 9 9 × 1 0 9 ) ( 1 1 × 1 0 − 6 ) 2 = 8 3 . 7 N .