Relativistic electron
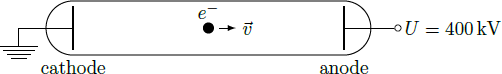
Within a vacuum tube, an electron is accelerated by a DC electrical voltage of U = 4 0 0 kV . Suppose the electron has zero velocity at the cathode. What is the final velocity v of the electron when it hits the anode?
The following constants could be helpful: Elementary charge Mass of an electron Speed of light e m e c ≈ 1 . 6 ⋅ 1 0 − 1 9 C ≈ 9 . 1 ⋅ 1 0 − 3 1 kg ≈ 3 ⋅ 1 0 8 m / s
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
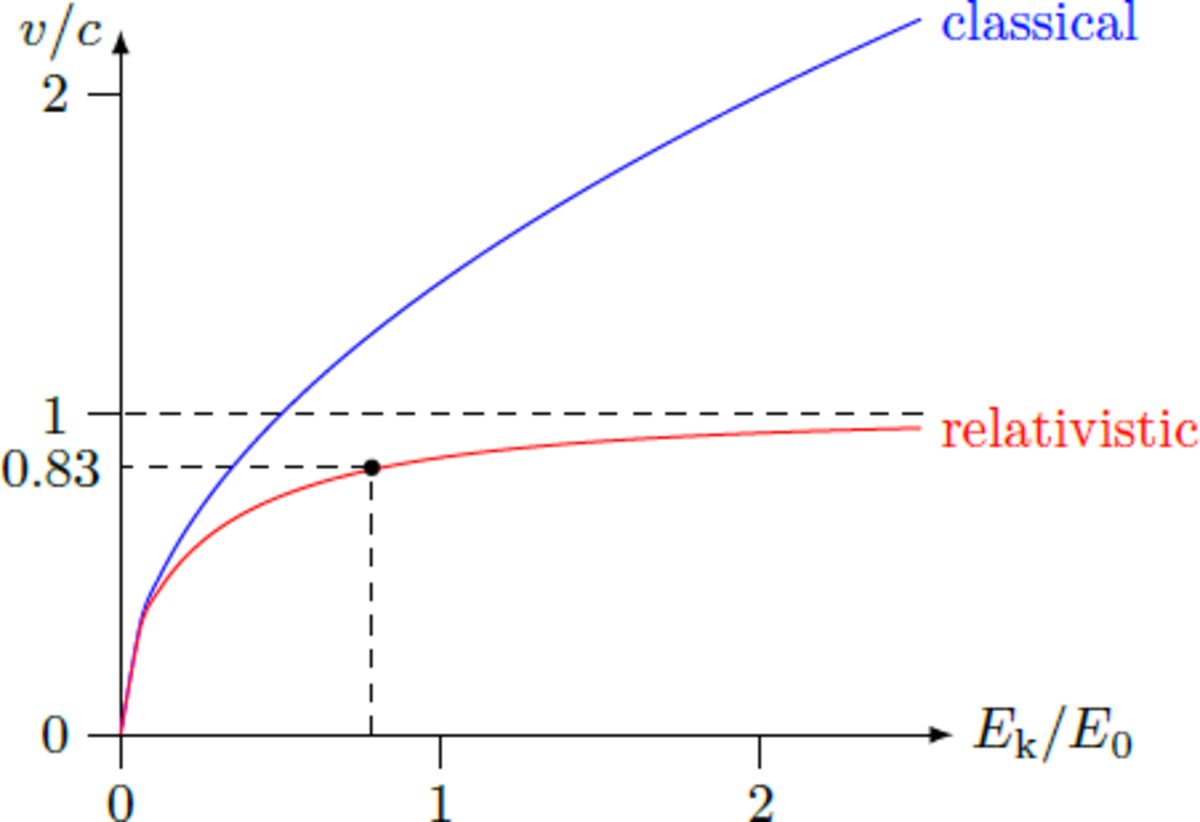
In an electric field of voltage U = 4 0 0 kV , the electron has at the cathode a potential energy E pot = e U = 4 0 0 keV ≈ 6 . 4 ⋅ 1 0 − 1 4 J The rest energy of an electron results according to Einstein E 0 = m e c 2 ≈ 8 . 2 ⋅ 1 0 − 1 4 J ≈ 5 1 1 keV Since the potential energy of the electron is comparable in magnitude to the rest energy, we need relativistic mechanics. The kinetic energy of the electron then is E kin = m c 2 − m e c 2 = 1 − ( v / c ) 2 m e c 2 − m e c 2 where m denotes the relativistic mass of the electron. In the case of low velocities ( v / c ≪ 1 ), the classical approximation for the kinetic energy applies: E kin ≈ 2 m e v 2 + O ( ( v / c ) 4 ) In our case, however, we must take into account the relativistic corrections. When the potential energy is converted into kinetic energy ( E kin = E pot ), it results ⇒ ⇒ ⇒ ⇒ e U ε : = m e c 2 e U ε + 1 1 1 − ( ε + 1 ) 2 1 v = 1 − ( v / c ) 2 m e c 2 − m e c 2 = 1 − ( v / c ) 2 1 − 1 = 1 − ( v / c ) 2 = ( v / c ) 2 = c 1 − ( ε + 1 ) 2 1 = c 1 − ( e U / ( m e c 2 ) + 1 ) 2 1 Insertion of the numerical values yields v ≈ 0 . 8 3 ⋅ c ≈ 2 . 5 ⋅ 1 0 8 m/s The graph below compares the velocity for the classical and the relativistic case as a function of kinetic energy