Remainder of polynomial division
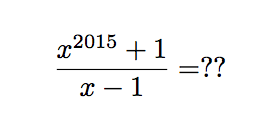 What is the remainder of the division of
x
2
0
1
5
+
1
by
x
−
1
?
What is the remainder of the division of
x
2
0
1
5
+
1
by
x
−
1
?
Hint : This should take you no longer than 5 seconds to figure out the answer!
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Use the polynomial remainder theorem:
x 2 0 1 5 + 1 = ( x − 1 ) ( D ( x ) ) + R ( x ) , basically the expression is equal to x − 1 multiplied by some other number and add the remainder.
Substitute 1 for x so that ( x − 1 ) ( D ( x ) ) would equal to 0 . Doing so will leave us with the remainder:
1 2 0 1 5 + 1 = ( 1 − 1 ) ( D ( 1 ) ) + R ( 1 ) ⟶ 1 + 1 = R ( 1 ) ⟶ R ( 1 ) = 2
Therefore the remainder is 2
Let P ( x ) = x 2 0 1 5 + 1 and Q ( x ) = x − 1 . We want to find the remainder of Q ( x ) P ( x ) .
Now, we can write P ( x ) as the sum of two polynomials R ( x ) and S ( x ) , such that: R ( x ) = x 2 0 1 5 − 1 and S ( x ) = 2 . Notice that, since R ( x ) has 1 as a root, it can be divided by Q ( x ) ; thus, P ( x ) ≡ S ( x ) ( m o d x − 1 ) , and so 2 is the remainder sought.
what happens when x=2? Remainder is 0, right?
Log in to reply
Well, polynomial modular arithmetic works almost in the same way as regular modular arithmetic. The key difference lies on the fact we're searching for the remainder of the polynomial division, not the actual value of the division itself when you plug in a value; when you say x = 2 , you're merely stating that 2 2 0 1 5 + 1 ≡ 2 ( m o d 1 ) , which is not much of a big deal because every integer divided by one equals itself and leaves no remainder at all.
What I stated was that there is some polynomial T ( x ) such that the following equation is true for all x:
P ( x ) = T ( x ) ∗ ( x − 1 ) + 2
The remainder of the polynomial division is two, that's all.
Let q ( x ) , r ( x ) ∈ C [ X ] be the quotient and remainder of this division. respectively Then, we may write : x 2 0 1 5 + 1 = q ( x ) ( x − 1 ) + r ( x ) ( † ) The trick is NOT to try figuring out what q ( x ) is. To be honest, even as I finished setting up this little exercise, I had (and still have) no idea what the quotient looks like, nor am I sufficiently bored to calculate it!
All that we need to notice is that de g ( r ) < 1 , which is to say that r ( x ) is a constant! So, we might as well set : r ( x ) ≡ c .
Since the value is the same ∀ x , we can evaluate ( † ) for x ≡ 1 .
We easily get that : c = 2
however 1, 2, 3 shall not satisfy the value of x
x - 1 definitely divides x to the 2015 minus 1. Therefore x 2015 + 1 has a remainder of 2.
if x-1 divides p(x)= x^2015 then put x-1=0 .it implies x=1. put x=1 in p(x) .then answer is 1.
just put one for x and add a negative sign, then add
use remainder theorem. Substitute 1 to the equation