Remember the aim in archery?
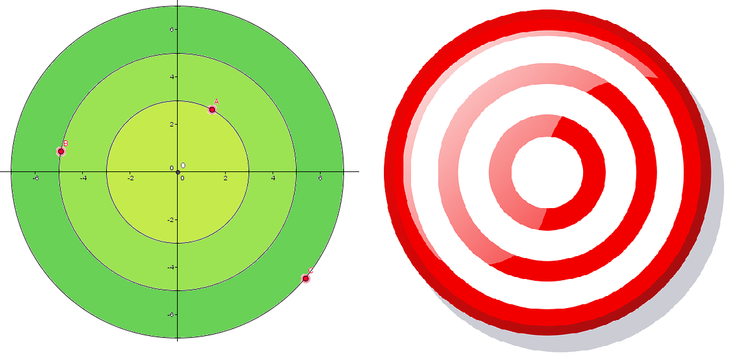 There are 3 concentric circles with center
O
and radii
3
,
5
,
7
units.
There are 3 concentric circles with center
O
and radii
3
,
5
,
7
units.
Points A , B , C are on these circles, one on each circle.
Find the maximum value of A B 2 + B C 2 + C A 2 in sq. units.
Also see
C'mon! Archery is irrelevant here!
The answer is 249.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Well, actually I did it just by taking direct values and after I saw Hari's solution, I just saw that there is a general case.
Log in to reply
What are the values for which equality is reached? I can't figure out what the conditions for equality in your proof are.
Log in to reply
Differentiate this - 2 a b 2 + c 2 + b c c o s ( y ) − 2 b c c o s ( y ) w.r.t. to y and equate to 0 , you get the value of y fr which the equation satisfies. The value of x is found as a c o s x + b s i n x = R s i n ( x − α ) and so on.
And z is just 2 π − x − y , so you get the equality conditions which depend on the angles.
In a triangle ABC and for a point in space,there is inequality
A B 2 + B C 2 + C A 2 is less than or equal to 3( P A 2 + P B 2 + P C 2 )
Now if we take the point P to be the center then the rest is easy......
But from what I see so far, then 249 is an upper bound. How to show the value is actually achieved?
where do you find this inequality?
Log in to reply
I learned it in vectors lesson....
Log in to reply
Thaks... I tried and did it using geometry
@Hari prasad Varadarajan I have shared the proof!
Log in to reply
That's great....
Nicely done, thanks.
Well, the inequality Hari prasad Vardarajan has given is correct and the following is the proof -
P A = a , P B = b , P C = c , A P B = x , B P C = y , C P A = z
Using cosine rule,
A B 2 + B C 2 + C A 2 = 2 ( a 2 + b 2 + c 2 ) − 2 a b c o s ( x ) − 2 b c c o s ( y ) − 2 c a c o s ( z )
= 2 ( a 2 + b 2 + c 2 ) − 2 a b c o s ( x ) − 2 b c c o s ( y ) − 2 c a ( c o s ( 2 π − ( x + y ) ) ) [ x + y + z = 2 π ]
= 2 ( a 2 + b 2 + c 2 ) − 2 a b c o s ( x ) − 2 b c c o s ( y ) − 2 c a c o s ( x ) c o s ( y ) + 2 c a s i n ( x ) s i n ( y )
= 2 ( a 2 + b 2 + c 2 ) − c o s ( x ) ( 2 a b + 2 c a c o s ( y ) ) + s i n ( x ) ( 2 c a s i n ( y ) ) − 2 b c c o s ( y )
= 2 ( a 2 + b 2 + c 2 ) + c o s ( x ) ( − 2 a b − 2 c a c o s ( y ) ) + s i n ( x ) ( 2 c a s i n ( y ) ) − 2 b c c o s ( y )
We know a c o s ( x ) + b s i n ( x ) has maximum at a 2 + b 2
≤ 2 ( a 2 + b 2 + c 2 ) + ( 2 a b + 2 c a c o s ( y ) ) 2 + ( 2 c a s i n ( y ) ) 2 − 2 b c c o s ( y )
≤ 2 ( a 2 + b 2 + c 2 ) + 4 a 2 b 2 + 4 c 2 a 2 c o s 2 ( y ) + 4 a 2 b c c o s ( y ) + 4 a 2 c 2 s i n 2 ( y ) − 2 b c c o s ( y )
≤ 2 ( a 2 + b 2 + c 2 ) + 4 a 2 b 2 + 4 c 2 a 2 ( c o s 2 ( y ) + s i n 2 ( y ) ) + 4 a 2 b c c o s ( y ) − 2 b c c o s ( y )
≤ 2 ( a 2 + b 2 + c 2 ) + 4 a 2 ( b 2 + c 2 ) + 4 a 2 b c c o s ( y ) − 2 b c c o s ( y )
≤ 2 ( a 2 + b 2 + c 2 ) + 2 a b 2 + c 2 + b c c o s ( y ) − 2 b c c o s ( y )
If we take derivative of the second part of the above equation involving y w.r.t. y , we get where the equality will hold and the maximum which will just be a 2 + b 2 + c 2
After adding, we get
A B 2 + B C 2 + C A 2 ≤ 3 ( a 2 + b 2 + c 2 )