Polygon with increasing angles
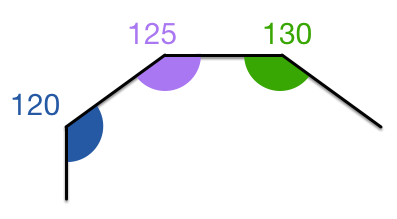
The interior angles of a convex polygon are in arithmetic progression . The smallest angle is and the common difference is .
Find the number of sides of the polygon.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let there be n sides of the polygon. Then the sum of its interior angles is given by
S n = ( n − 2 ) × 1 8 0 ∘ .
Also, the sum of all the terms of an arithmetic progression is given by
S n = 2 n [ 2 a 1 + ( n − 1 ) d ] where a 1 = 1 2 0 ∘ and d = 5 ∘
Equating both the equations:
( n − 2 ) × 1 8 0 ∘ = 2 n [ 2 a 1 + ( n − 1 ) d ]
On solving, we will get two values for n ⇒ 1 6 , 9
But if the polygon is of 16 sides, the 1 3 t h angle will be 1 8 0 ∘ , which is not allowed.
Hence, the answer is ⇒ 9