Reminds Me of Mickey Mouse

Geometry Level 3

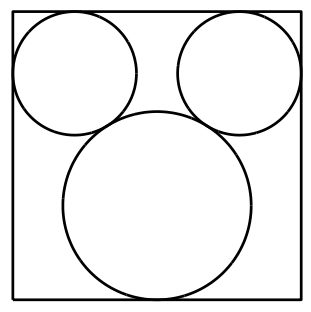Three circles fit inside a square as shown where two small circles touch a large circle. Given that the radius of the small circles is 3 and the side length of the square is 14, find the radius of the larger circle to one decimal place.


The answer is 4.6.

Mark Mottian by Mark Mottian , 22, South Africa

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Mark Mottian
Aug 5, 2015

Let R R be the radius of the larger circle. Notice that the red triangle is isosceles.

After using Pythagoras: ( 11 − R ) 2 + 4 2 = ( 3 + R ) 2 (11-R)^{2} + 4^{2} = (3+R)^{2}

Solving gives R = 32 7 = 4.6 R = \frac {32}{7}= \boxed{4.6}

Click here to access image.
14 Helpful 0 Interesting 0 Brilliant 0 Confused

Why are the following three points collinear?

  • Centre of larger circle
  • Point of contact between the larger circle and the smaller circle
  • Centre of smaller circle

Kenny Lau - 5 years, 10 months ago

Log in to reply

Those points of any two circles touching each other will satisfy collinearity. They're touching each other so they have common tangent and also common normal passing through the point of contact. So they're collinear. If you still are not satisfied, just take some convenient coordinate system to locate those three points by taking radii as variables and you can see that the area of triangle formed by those points is zero.

suneesh jacob - 5 years, 10 months ago

I used a simpler approach though not rigorous I got the answer. From just observing I proved that

4<R<5 Also R lies towards the middle of the interval so I tried 4.5 and then 4.6

Prabhav Jain - 5 years, 10 months ago

I used a different approach, based on the assumption that the lines connecting the small and large circles is always 45ª. This gives a wrong answer, however, I cannot see why the assumption is wrong.

Javier Gómez - 5 years, 10 months ago

I have my solution to show different approach but your is better and have voted for yours.

Niranjan Khanderia - 3 years ago

Did the same!

Atomsky Jahid - 5 years ago
William Isoroku
Aug 8, 2015

Let x x equal the radius of the big ass circle. By doing some math, we get:

x 2 + 6 x − 7 + x + 3 = 14 \sqrt{x^2+6x-7}+x+3=14

This gives us x = 4.6 \boxed{x=4.6}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...