Repeating Decimal in Base k
For some positive integer k , the repeating base- k representation of the base-ten fraction 3 9 5 is 0 . 3 5 k = 0 . 3 5 3 5 3 5 3 5 3 5 3 5 ⋯ k . What is k ?
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I had gone to 2nd last line but then I did silly mistake...
A repeating decimal in base- k has the form k A + k 2 B + k 3 C + ⋯ . This repeating decimal with look like this: k 3 + k 2 5 + k 3 3 + k 4 5 + k 5 3 + ⋯ Separating it out: k 3 + k 2 3 + k 3 3 + k 4 3 + k 4 3 + k 5 3 + ⋯ + k 2 2 + k 4 2 + k 6 2 + ⋯ Factoring out the numerator: 3 ( k 1 + k 2 1 + k 3 1 + k 4 1 + ⋯ ) + 2 ( k 2 1 + k 4 1 + k 6 1 + ⋯ ) Changing the last part: 3 ( k 1 + k 2 1 + k 3 1 + k 4 1 + ⋯ ) + 2 ( ( k 2 ) 1 + ( k 2 ) 2 1 + ( k 2 ) 3 1 + ( k 2 ) 4 1 + ⋯ ) Now, we know that 1 + r + r 2 + r 3 + r 4 + r 5 + ⋯ = 1 − r 1 , if 0 < r < 1 . Because k is a positive integer greater than 1 (as base 1 would just be unary, a series of only 1 's), 0 < k 2 1 < k 1 < 1 , so this formula applies. However, we are missing the starting 1 in both equations, but we can just subtract it out. 3 ( k 1 + k 2 1 + k 3 1 + k 4 1 + ⋯ ) + 2 ( ( k 2 ) 1 + ( k 2 ) 2 1 + ( k 2 ) 3 1 + ( k 2 ) 4 1 + ⋯ ) 3 ( 1 − k 1 1 − 1 ) + 2 ( 1 − k 2 1 1 − 1 ) 3 ( k − 1 k − k − 1 k − 1 ) + 2 ( k 2 − 1 k 2 − k 2 − 1 k 2 − 1 ) 3 ( k − 1 1 ) + 2 ( k 2 − 1 1 ) We are told that this equals 3 9 5 : 3 ( k − 1 1 ) + 2 ( k 2 − 1 1 ) = 3 9 5 k − 1 3 + k 2 − 1 2 = 3 9 5 ( k − 1 ) ( k + 1 ) 3 ( k + 1 ) + k 2 − 1 2 = 3 9 5 k 2 − 1 3 k + 3 + k 2 − 1 2 = 3 9 5 ( k 2 − 1 ) 3 k + 5 = 3 9 5 1 1 7 k + 1 9 5 = 5 k 2 − 5 5 k 2 − 1 1 7 k − 2 0 0 = 0 k = 2 ( 5 ) 1 1 7 ± 1 1 7 2 + 4 ( 2 0 0 ) ( 5 ) = − 1 . 6 , 2 5 And because k is a positive integer k = 2 5
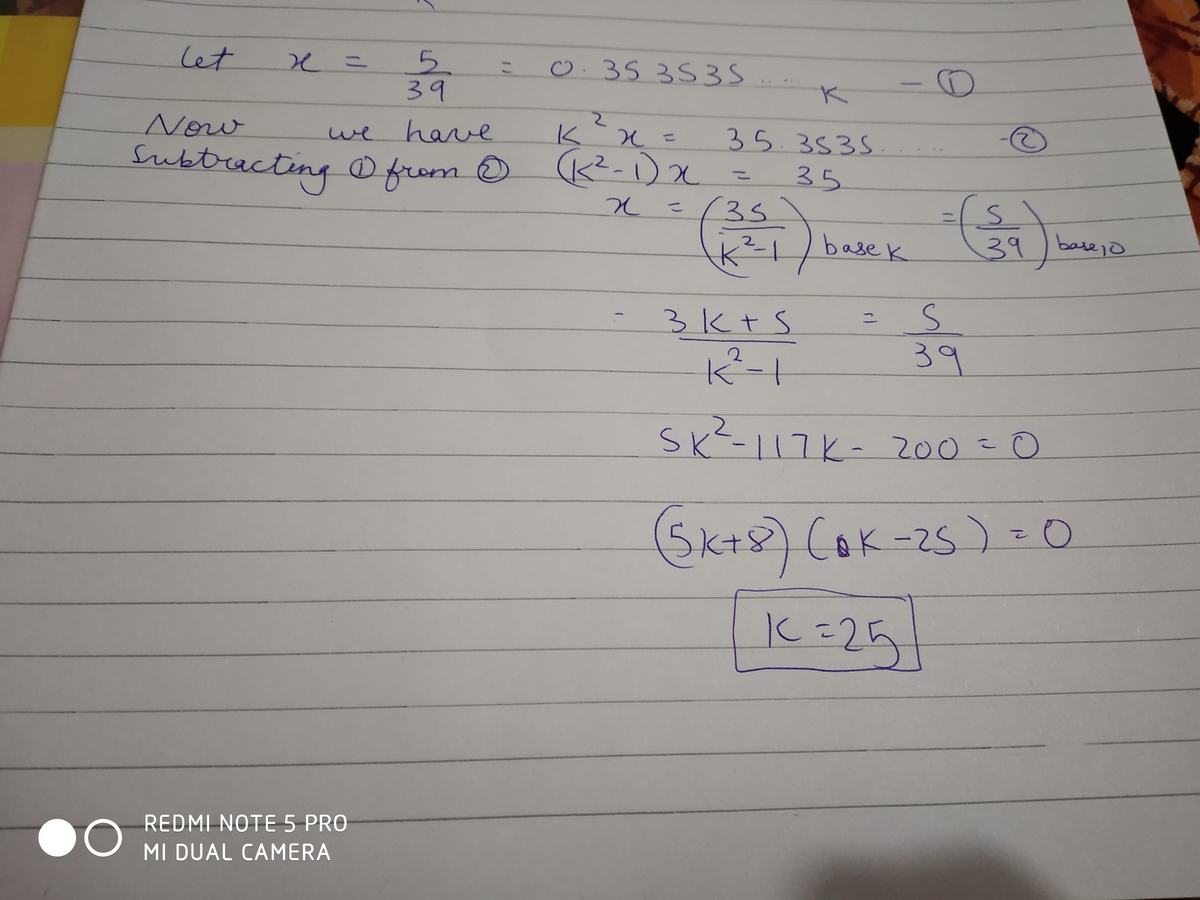
Similar explanation with @Joshua Lowrance 's
Based on how number system work, we have:
0 . 3 5 k = ( k 3 + k 2 5 + k 3 3 + k 4 5 + ⋯ ) 1 0 = ( 3 9 5 ) 1 0
Therefore in base-10,
n = 1 ∑ ∞ k n 3 + n = 1 ∑ ∞ k 2 n 2 k 3 ( 1 − k 1 1 ) + k 2 2 ( 1 − k 2 1 1 ) k − 1 3 + k 2 − 1 2 k 2 − 1 3 ( k + 1 ) + 2 k 2 − 1 3 k + 5 1 1 7 k + 1 9 5 5 k 2 − 1 1 7 k − 2 0 0 ( 5 k + 8 ) ( k − 2 5 ) ⟹ k = 3 9 5 = 3 9 5 = 3 9 5 = 3 9 5 = 3 9 5 = 5 k 2 − 5 = 0 = 0 = 2 5 Since k is an integer.