Required: surface area
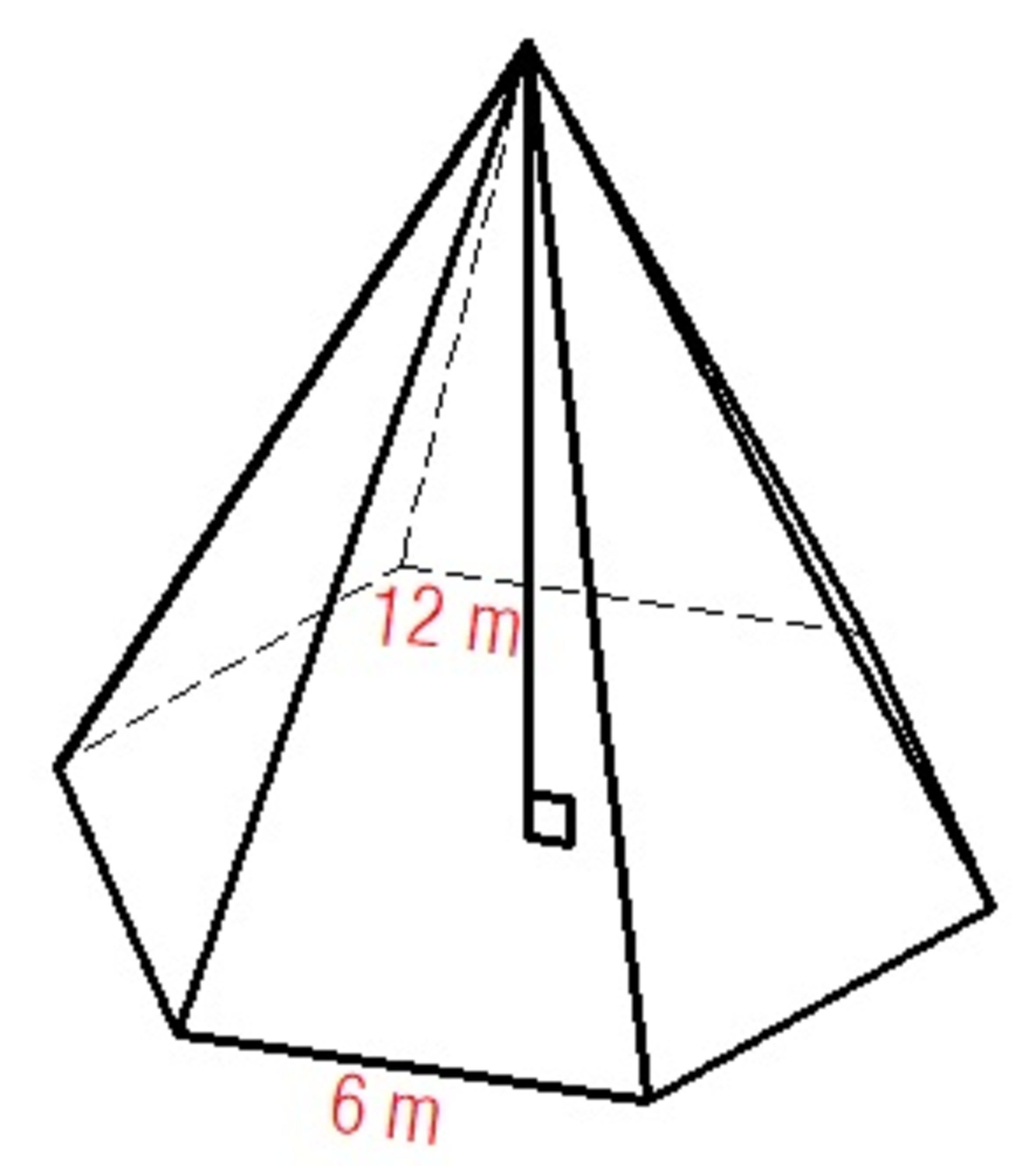 Shown in the figure is a regular pyramid with a height of
. The base is a regular hexagon with an edge length of
. Find the surface area of the pyramid in
. If your answer can be expressed as
, where
and
are positive co-prime integers, submit
.
Shown in the figure is a regular pyramid with a height of
. The base is a regular hexagon with an edge length of
. Find the surface area of the pyramid in
. If your answer can be expressed as
, where
and
are positive co-prime integers, submit
.
The answer is 76.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Surface Area - Problem Solving
The surface area is equal to the lateral area (sum of the areas of the triangles) plus the area of the hexagon. The lateral area is 2 1 P L where P is the perimeter of the base and L is the slant height. The area of the hexagon is 2 3 3 x 2 where x is the edge length of the hexagon. Thus,
A = 2 1 ( 6 ) ( 6 ) ( 3 1 9 ) + 2 3 3 ( 6 2 ) = 5 4 1 9 + 5 4 3 = 5 4 ( 1 9 + 3 )
So the desired answer is a + b + c = 5 4 + 1 9 + 3 = 7 6