Resistance Network (Part 5)
If the squares have side length , and the wire has a resistance of per unit length, what is the equivalent resistance between the two colored dots?
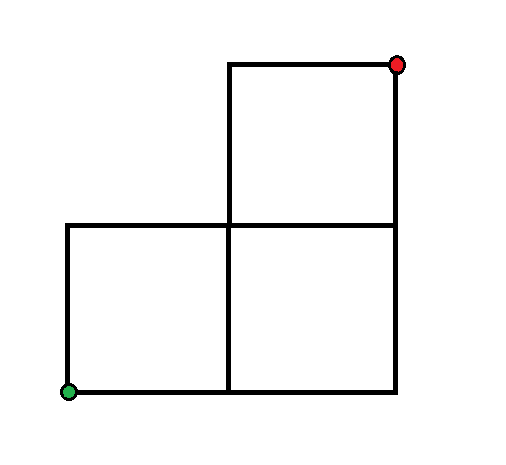
The answer is 1.7143.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We note that resistance network is symmetrical about the line C C ′ . Then ∣ V A C ∣ = ∣ V B C ∣ = ∣ V A C ′ ∣ = ∣ V B C ′ ∣ = 2 1 ∣ V A B ∣ . This means that point C and point C ′ are equipotential and can be considered as a single point C . The equivalent circuit for the resistance network is as the right figure. The equivalent resistance is given by:
R A B = 2 ( 2 ∣ ∣ ( 1 + 1 ∣ ∣ 1 ) ) = 2 ( 2 ∣ ∣ ( 1 + 2 1 ) ) = 2 ( 2 ∣ ∣ 2 3 ) = 7 1 2 ≈ 1 . 7 1 4 Ω