Resistance Network
In the figure, the black wire has a resistance of 1 Ω per unit length. The four small black squares each have side length 1 , and the four slanted black segments each have length 2 .
The resistance network is connected to a DC voltage source by green and red wire segments; both of which have zero resistance.
Any intersection between two line segments should be interpreted as an electrical connection. The only exception to this is that the red wire only connects to one of the battery terminals, and to the center of the resistance network (ignore the intermediate intersections of the red wire).
What overall resistance does the black wire network present to the voltage source?
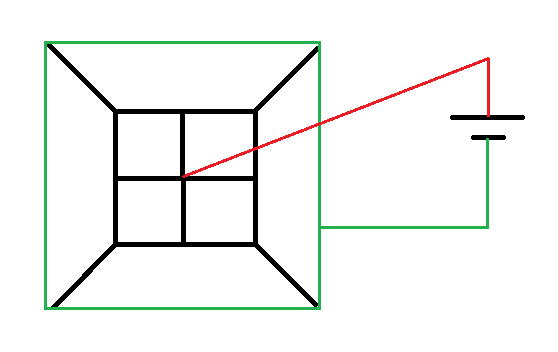
The answer is 0.875.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thanks, that's a nice way of doing it
I want to reduce my presence on Brilliant, but I cannot resist to your problems, they are so good.
Thanks, I appreciate that. May I ask why you wish to leave? I've been hearing things like that from several people, and it kind of saddens me to hear it. I've noticed that the "community" section seems to be fading away a bit.
I am a bit tired of seeing so many factual errors in the physics questions. I think the editors pretty much abandoned the community section.
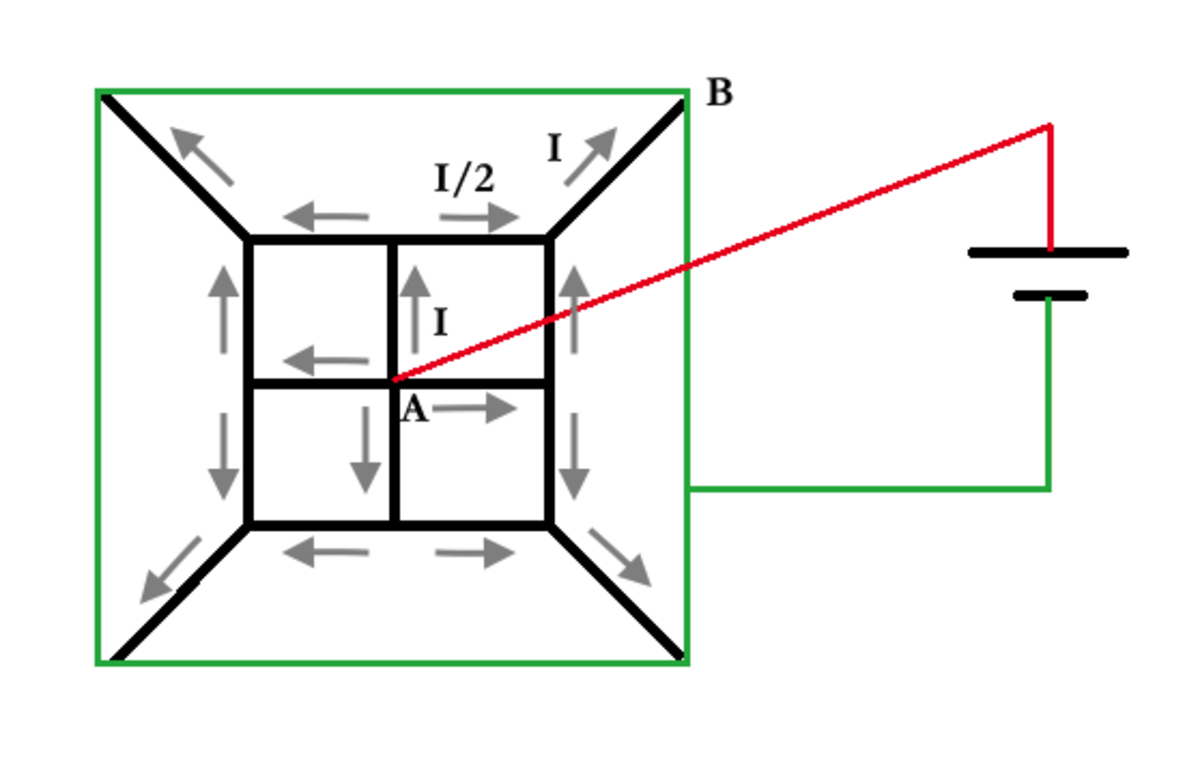
-
Use the symmetry to find the relationship between the different intensities.
-
Calculate the tension drop from A to B using Ohm's Law: V = 1 ⋅ I + 1 ⋅ 2 1 I + 2 ⋅ I = 2 7 I
-
The overall resistance is the quotient of this voltage and the total intensity, which is 4 I : R = 4 I 2 7 I = 8 7 Ω
Cut the network into four parts, so that the each part has a small square and one of the slanted segments. In order to do the cut in a symmetric way we have to split the four wires (that make a cross shape) along their length. Therefore the resistance of each of the split wires will be 2 Ohm.
Each one of the parts we obtained can be represented as two wires of 2 Ohms in parallel, connected in series with two wires of 1 Ohm, connected in series with the original 2 Ohm wire. The total resistance of each one of these networks is 3.5 Ohm. When we re-connect them into the original structure they will be connected parallel to each other, so the final resistance is 3.5 Ohm/4=0.874 Ohm.