Resistance of a circular segment!
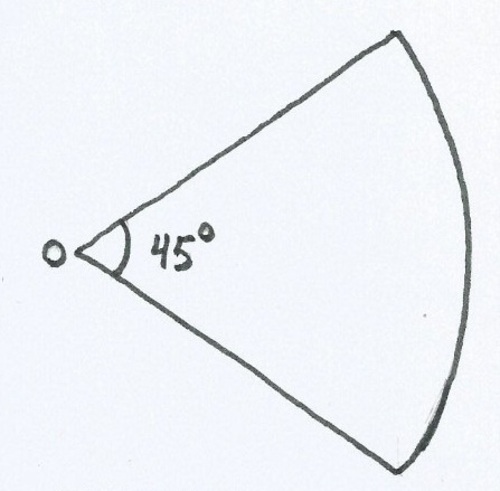 A part of circular plate of thickness
t
and radius
a
is as shown in the figure. Resistivity of the material varies as
ρ
=
ρ
0
r
where
ρ
0
is a constant and
r
is the distance from center O. The resistance between center O and the curved surface is:
A part of circular plate of thickness
t
and radius
a
is as shown in the figure. Resistivity of the material varies as
ρ
=
ρ
0
r
where
ρ
0
is a constant and
r
is the distance from center O. The resistance between center O and the curved surface is:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
Good standard solution. Can this be result obtain without an integration step?
Let's divide the plate into infinite parallel differential conic wires of length a , thickness t and width of r d θ at a point with distance r from the center O . The resistance of a differential section of length d r of the wire at a distance r from the center O is ρ A l , where l is the length of the section and A is its area, therefore ρ A l = ρ o r r t d θ d r = ρ o t d θ d r . Integrating over the differential wire we obtain its resistence: d R = 0 ∫ a t d θ ρ o d r = t d θ ρ o a The conductance of the differential wire is: d G = d R 1 = ρ o a t d θ The total conductance of the plate is: G = 0 ∫ 4 π ρ o a t d θ = 4 ρ o a π t Finally, the total resistence of the plate is: R = G 1 = π t 4 ρ o a
The small change in resistance Δ R at r is given by Δ R = A ρ Δ r , where A is the curved cross-sectional area A = 3 6 0 ∘ 4 5 ∘ × 2 π r t = 4 π r t . Therefore,
Δ R = π r t 4 ρ Δ r ⇒ ∫ 0 a π r t 4 ρ d r = ∫ 0 a π r t 4 ρ 0 r d r = ∫ 0 a π t 4 ρ 0 d r = π t 4 ρ 0 a