Resistance of Four Rings
A uniform wire of resistance is cut into four circular rings of equal radius. Rings are then connected such that their centers lie on the vertices of a square (as illustrated in the figure above).
If the equivalent resistance between and can be expressed as , where and are coprime positive integers, determine the value of .
The answer is 143.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Moderator note:
In this particular circuit, there is a high degree of symmetry that we can exploit to sidestep some of the calculations and get to some of the findings earlier in the process.
Steven points out that two of the wire sections are dead in that they carry no voltage.
If we were to fold the circuit across an axis of symmetry (as below), we see that those sections are transformed into wires that do not connect to another place in the circuit.
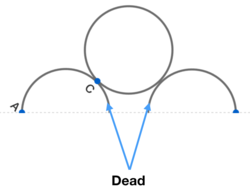This implies that in the original layout, both of those wire's ends are at the same potential, no current flows down them, and they can be safely ignored.
From this view, we can also see that the circuit can be simplified to two wire sections in series with a ring. The only adjustment we'd need to make is to replace each circuit element (e.g. the wire sections and the loop) by an equivalent element that is the original element in parallel with itself. In this way, we can offload a little more of the calculation to origami.
Relevant wiki: Series and parallel resistors
There are four identical rings and the total resistance of them is R . Therefore, the resistance of one of the ring is 4 R .
Now, let us consider one of the rings,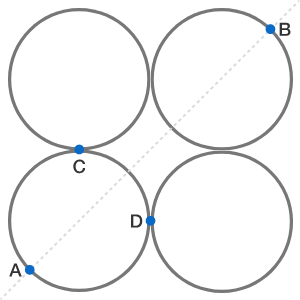
The length of C D is one-fourth whereas the length of both A C and A D are 3 / 8 of the perimeter of the ring. Therefore, the resistance of C D is 1 6 R and of A C and A D are 3 2 3 R .
Similarly, we can for the other rings and draw the following diagram.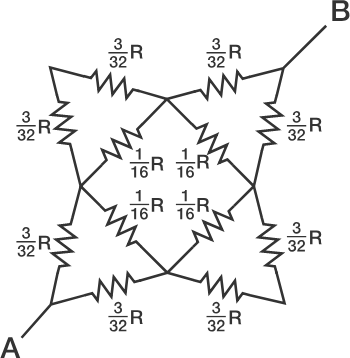
Grouping the resistors in series and parallel, we will get
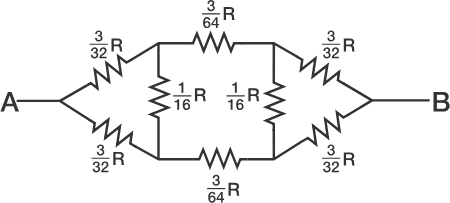
The circuit is symmetric and the top and the bottom branches are identical. Therefore, from symmetry, we can say that the potential drop across the two resistors of 1 6 R is zero. Hence, removing the two resistors and redrawing the circuit.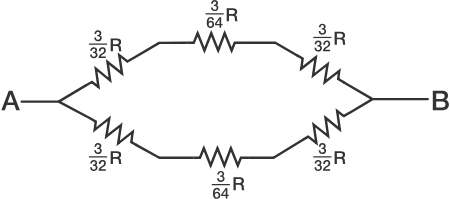
Now, connecting the resistors in one branch in series and resultant of the two branches in parallel, we get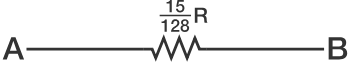
Comparing, b a R = 1 2 8 1 5 R , we get a = 1 5 , b = 1 2 8 . Therefore our answer, a + b = 1 4 3 .