Resistance of rings
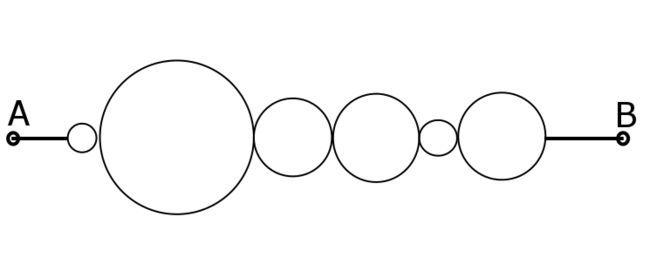 A wire of resistance
and length
is divided into six rings of radius in ratio
. The resistance between two terminals is of the form
, find
.
A wire of resistance
and length
is divided into six rings of radius in ratio
. The resistance between two terminals is of the form
, find
.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Extend the ray A towards B to make the line pass through the centre of circles and finally reach B take this the line of symmetry now on the part of it we have half the length of our original wire and the other half below it. So as R is proportional to length so the resistance of upper wire is R / 2 and the lower wire is also R / 2 and they are in parallel so the answer yields R / 4 .
a = 1 b = 4
The answer is 5