Resistant Infinite ladder
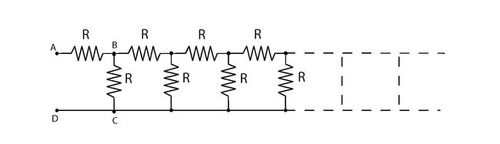 In the figure above, the effective resistance between the points
A
and
D
of the infinite ladder can be represented as
2
a
+
b
c
R
, where
c
is square free.
In the figure above, the effective resistance between the points
A
and
D
of the infinite ladder can be represented as
2
a
+
b
c
R
, where
c
is square free.
Find the value of a + b + c + 2 .
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Probably (1+✓5)/2 is called the golden ratio....am I right?
Perfect solution!cheers!
@Nihar Mahajan This is a nice way of doing. But What I did was something like this. I started at the rightmost resistance, assuming there existed one. And from there I go on evaluating the equivalent resistances. Fun thing is if you do that you will see, that the terms 2 ohm, 3 / 2 ohm, 5 / 3 ohm, 8 / 5 ohm, ... and so on. But as we already know and have probably observed, this is the ratio of F n F n + 1 , where F are the Fibonacci numbers, and we need to find the limit of the ratio at n->infinity. But as we already know, that is, 2 1 + 5 .
When I did this problem first, it seemed to be a very surprising occurrence of Fibonacci in resistances. XD
Log in to reply
That is really a nice way, I solved it using the way Nihar did in his solution. However, this solution is really amazing!!
Yes , I also found out the relation F n F n + 1 , but at that time I didn't know how to evaluate limits , so the problem remained unsolved by me by this approach :P
Nicely done! Just like solving infinite series sum.
- P.S; I got mad and input − 1 as the answer and then understood my stupid mistake and hit the correct number!
Log in to reply
Thanks! Yes , it is like the technique of solving infinite series sum.
Nice Generalization !!
Yeah, you come across the golden ratio very frequently in math and science.
Let the resistance between A a n d D be r .As the ladder is infinite , r is also equivalent resistance of the ladder to the right of points B a n d C .So we can redraw the circuit like this:
Thus we can form an equation:
r = R + r + R r R ⇒ r R + r 2 = R 2 + 2 r R ⇒ r 2 − r R − R 2 = 0 ⇒ r = 2 R + R 2 + 4 R 2 ⇒ r = 2 1 + 5 R ⇒ a + b + c + 2 = 1 + 1 + 5 + 2 = 9