Resistors On A Dodecahedron

Electricity and Magnetism Level 3

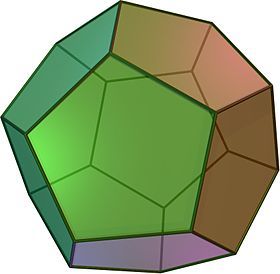
Each edge of a regular dodecahedron is a $1 \Omega$ resistor. If the effective resistance between two adjacent vertices can be represented as $\dfrac {a}{b} \Omega$ where $a$ and $b$ are co-prime positive integers, find $a + b$ .

A dodecahedron has 20 vertices and 30 edges with 3 edges meeting at each vertex.

Image credit: Wikipedia.

The answer is 49.

1 solution

Anupam Khandelwal
Feb 8, 2016

simply use the formula R=2(v-1)r/v.n

where v- total vertices;

         n- no. of edges meeting a vertex;
         r- resistance of an edge;

NOTE: one can use this formula to calculate equivalent resistance between any two adjacent vertices of a regular polyhedron

@Anupam Khandelwal This is a cool formula! (+1)

I wonder...

Does it apply to Archimedian Solids as well as Platonic solids?

And, is there a corresponding formula for opposite vertices?

Geoff Pilling - 4 years, 11 months ago

Thanks for the formula !!

Akshat Sharda - 5 years, 4 months ago

You must derive it

Yash Dev Lamba - 5 years, 4 months ago

Resistors On A Dodecahedron

Image credit: Wikipedia.

The answer is 49.

1 solution

0 pending reports