Resistor Network (4-10-2021)
A 1 0 volt DC source supplies a resistor network as shown. Each black line segment is a 1 Ω resistor (there are ten of these in total). The green wiring has no resistance.
If I S is the current flowing out of the source, give your answer as ( I S − 1 0 )
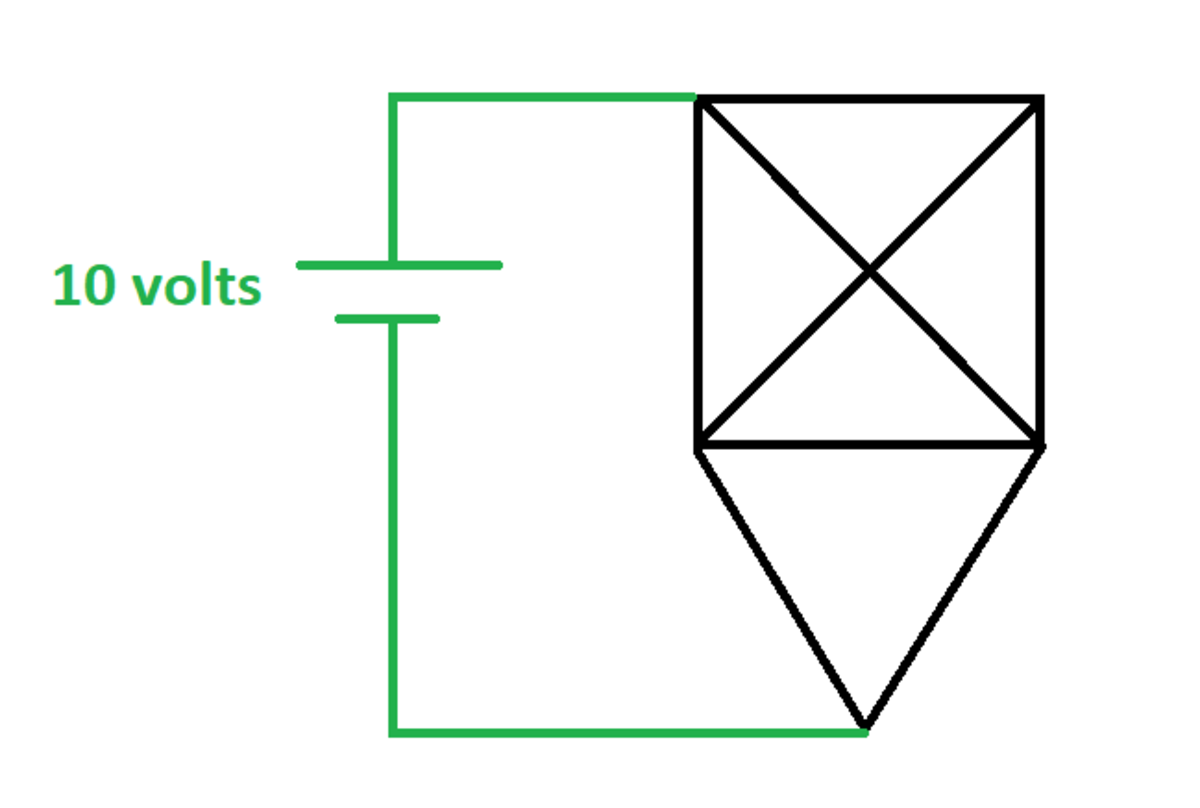
The answer is 0.3636.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I just brute forced it with KCL and KVL. Label the currents and loops as follows.
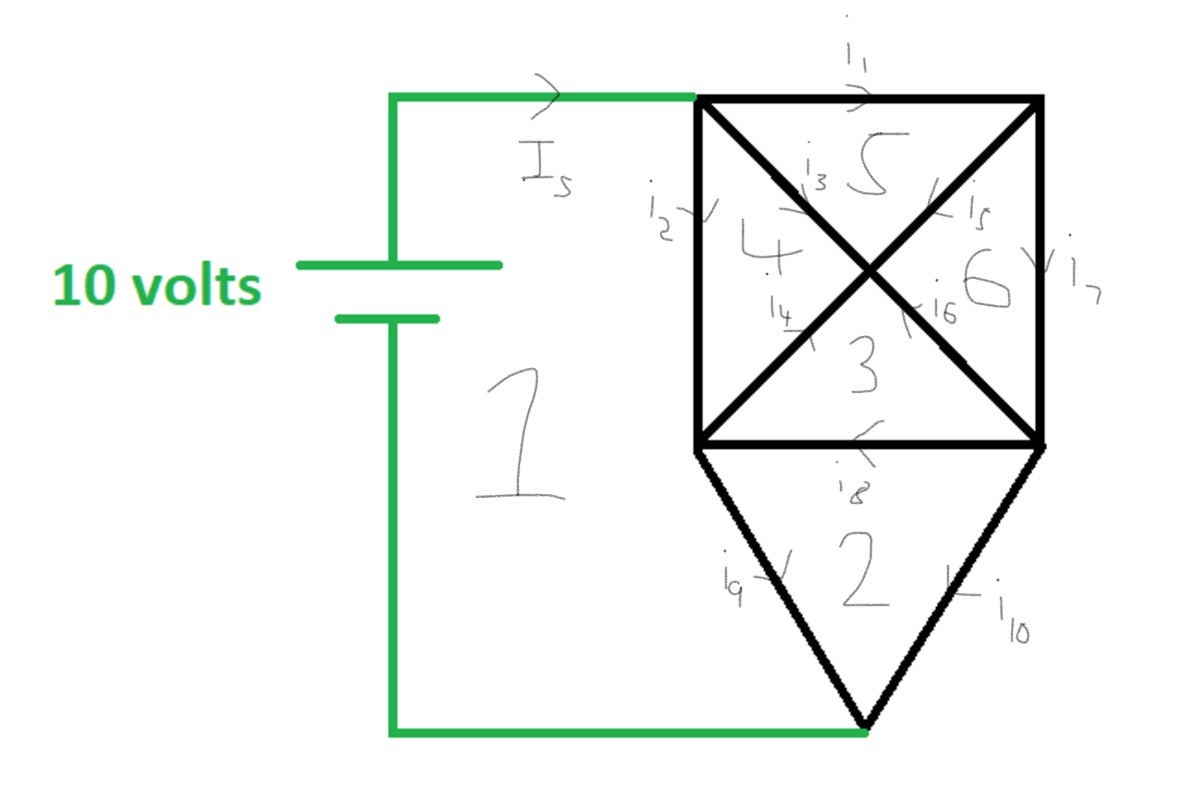
Using KCL at all of the nodes: I s − i 1 − i 2 − i 3 = 0 i 3 + i 4 + i 5 + i 6 = 0 i 1 − i 5 − i 7 = 0 i 2 − i 4 + i 8 − i 9 = 0 i 6 − i 7 + i 8 + i 1 0 = 0 I s − i 9 − i 1 0 = 0
Using KVL for all the loops, accounting for the fact that all grey wires have equal resistance of 1 Ω . For loops 1 through 6: i 2 + i 9 = 1 0 i 8 + i 9 − i 1 0 = 0 i 4 − i 6 + i 8 = 0 i 2 − i 3 + i 4 = 0 i 1 − i 3 + i 5 = 0 i 5 − i 6 + i 7 = 0
We have 12 equations and 11 unknowns, so one equation is linearly dependent (redundant) and must be eliminated. The one to be eliminated turns out to be the 6th equation. I made this educated guess from experience of solving the unbalanced Wheatstone bridge circuit, and it turned out to be correct here as well. It turns out that the 6th equation is a linear combination of the first five equations.
(
I
s
−
i
1
−
i
2
−
i
3
)
+
(
i
3
+
i
4
+
i
5
+
i
6
)
+
(
i
1
−
i
5
−
i
7
)
+
(
i
2
−
i
4
+
i
8
−
i
9
)
−
(
i
6
−
i
7
+
i
8
+
i
1
0
)
=
I
s
−
i
9
−
i
1
0
=
0
From here, we solve the system
M
i
=
b
, where
M
is a
1
1
×
1
1
matrix and
i
is the vector containing the currents of the circuit
i
=
⎝
⎜
⎜
⎜
⎛
i
1
⋮
i
1
0
I
s
⎠
⎟
⎟
⎟
⎞
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
|
Result:
1 |
|
Therefore, I s − 1 0 = 1 0 . 3 6 3 6 − 1 0 = 0 . 3 6 3 6
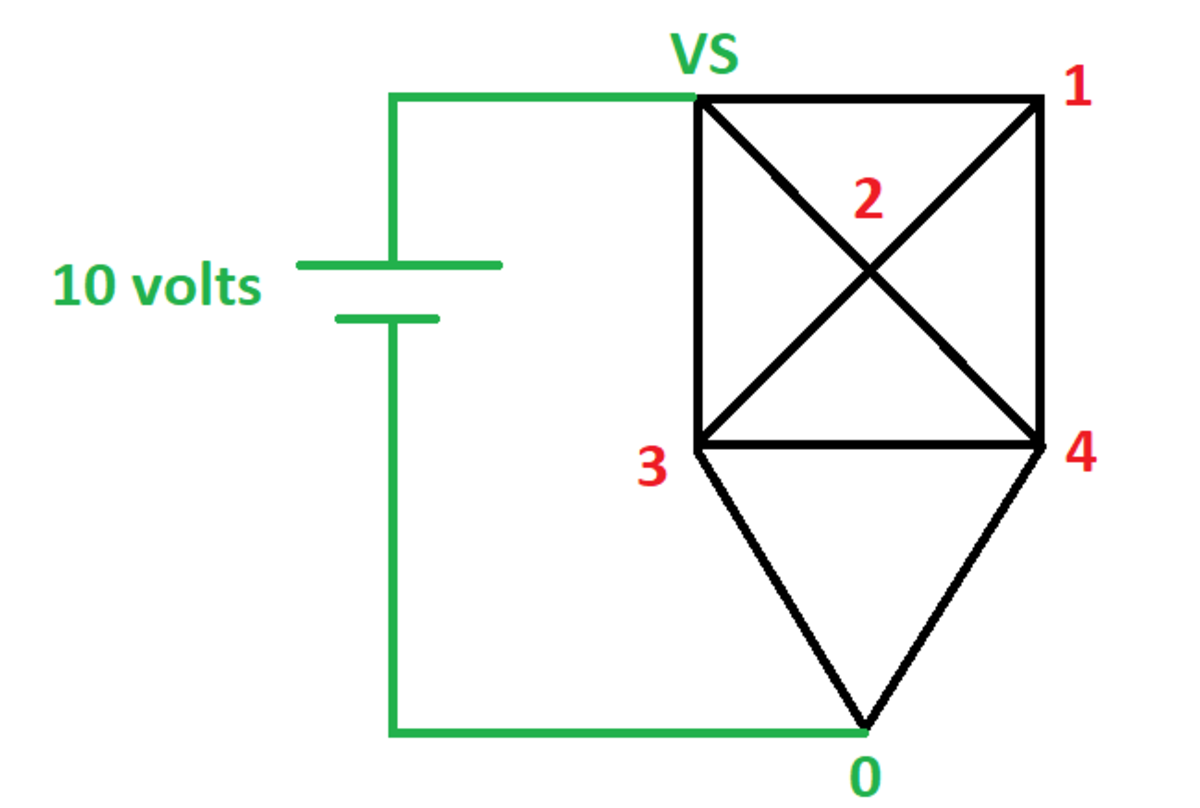
The solutions by @Charley Shi and @Karan Chatrath solve for currents, which certainly works. I generally prefer node equations over loop equations, and node equations are convenient in this case. Solving for node voltages results in four unknowns to solve for (labeled in the diagram). Find the node voltages such that the sum of currents out of each node is zero. Solving for the source current is easy once the node voltages are known.
I like using hill-climbing algorithms to solve these. The code is attached.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 |
|
@Steven Chase
Hello sir , How are you ?
Today I was just checking questions in Brilliant and I discovered that Brilliant is closing their community section.
How will you upload your problems?
Please reply me .
Thanks in advance.
Hello. Yes, that is quite a shock. I don't think there will be any more problems uploaded after that, so I will put one up each day until the community section is gone
Log in to reply
@Steven Chase
So how we will discuss problem after community section is gone ?
I want to download all your problems .
Currently I am busy for 2 months ,I was thinking that after 2 months ,I will discuss problems with you everyday .
But now how we will discuss problem after 2 months also?
I am thinking to make my own app for problem discussion after 2-3 months .
I want to invite you in my app for posting problem .
Do you have Telegram app.
Can we contact each other in that ? It is a very safe app.
Unknown currents indicated in the diagram. Circuit equations according to Kirchoff's laws are:
I 1 + I 2 + I 3 − I S = 0 I 1 − I 4 − I 5 = 0 I 2 + I 5 − I 6 − I 7 = 0 I 4 + I 6 − I 8 − I 9 = 0 I 7 + I 3 + I 8 − I 1 0 = 0 I 9 + I 1 0 − I S = 0 I 3 + I 1 0 = 1 0 I 2 + I 7 − I 3 = 0 I 4 − I 5 − I 6 = 0 I 5 + I 1 − I 2 = 0 I 6 + I 8 − I 7 = 0 I 9 − I 1 0 − I 8 = 0
This is a system of 12 equations and 11 unknowns. Therefore, one of the equations is redundant. To solve the system, any of the first 5 junction current equations can be left out of the computation and can be used later for a sanity check. The solution steps are left out and the final answer is:
I S − 1 0 = 0 . 3 6 3 6
I would not be surprised if there is a smarter way of solving this problem. Looking forward to seeing solutions apart from my 'brute force' approach.