Resistor Pyramid

Electricity and Magnetism Level 3

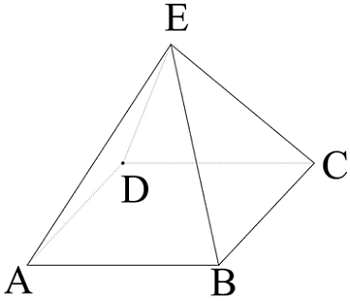
Jo has 8 identical resistors with resistance r r . He decides to build a Resistor Pyramid for his Physics project. Being a curious boy, he tries to find out the equivalent resistance between A A and B B using his ohmmeter. Find the equivalent resistance that the ohmmeter shows up when r = 1 Ω r = 1 \Omega .

If the resistance can be expressed in the form of α β \dfrac{\alpha}{\beta} , where α \alpha and β \beta care coprime positive integers, submit your answer as α + β \alpha + \beta .


The answer is 23.

Swapnil Das by Swapnil Das , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

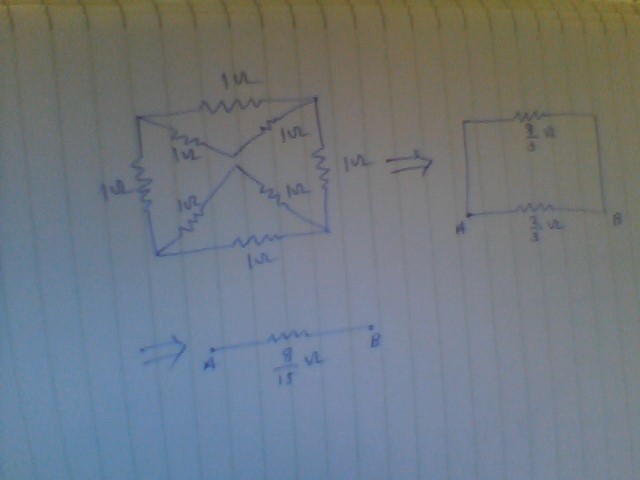
Relevant wiki: Series and parallel resistors

Let's take a top view of the pyramid,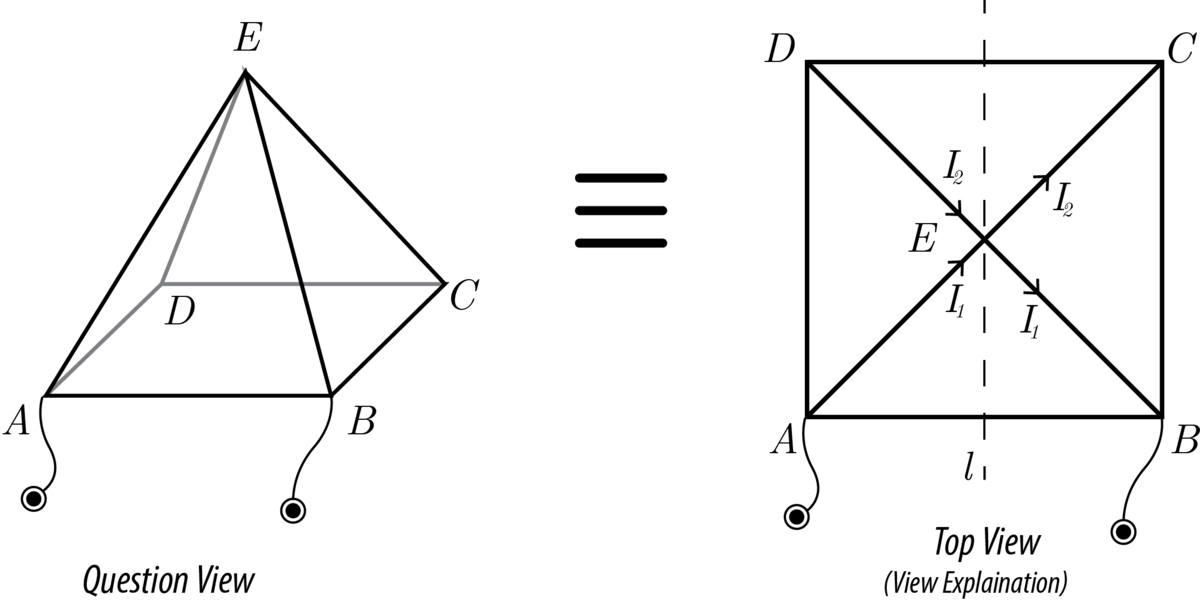

Now, since the connections are symmetric about ℓ \ell , we can split the connections at point E E to give,

Now it's a simple circuit, which after computing the net resistance gives R e q = 1 1 + 1 2 + 1 2 + 1 1 + 1 2 = 8 15 R_{\mathrm{eq}} = \dfrac 1{1+\dfrac12+\dfrac1{2+\dfrac1{1+\dfrac12}}}=\boxed{\dfrac8{15}}

10 Helpful 0 Interesting 1 Brilliant 0 Confused

Moderator note:

Always best to let a well made figure do the talking. This is exceptionally clear.

Thanks! That's very clearly presented :)

Calvin Lin Staff - 5 years ago

Very nicely done :)

Abhay Tiwari - 5 years ago
Swapnil Das
May 27, 2016

The very resistor pyramid can be transformed to the following, and then easily evaluated by the disconnection method.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Did the exact same

Aditya Kumar - 5 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...