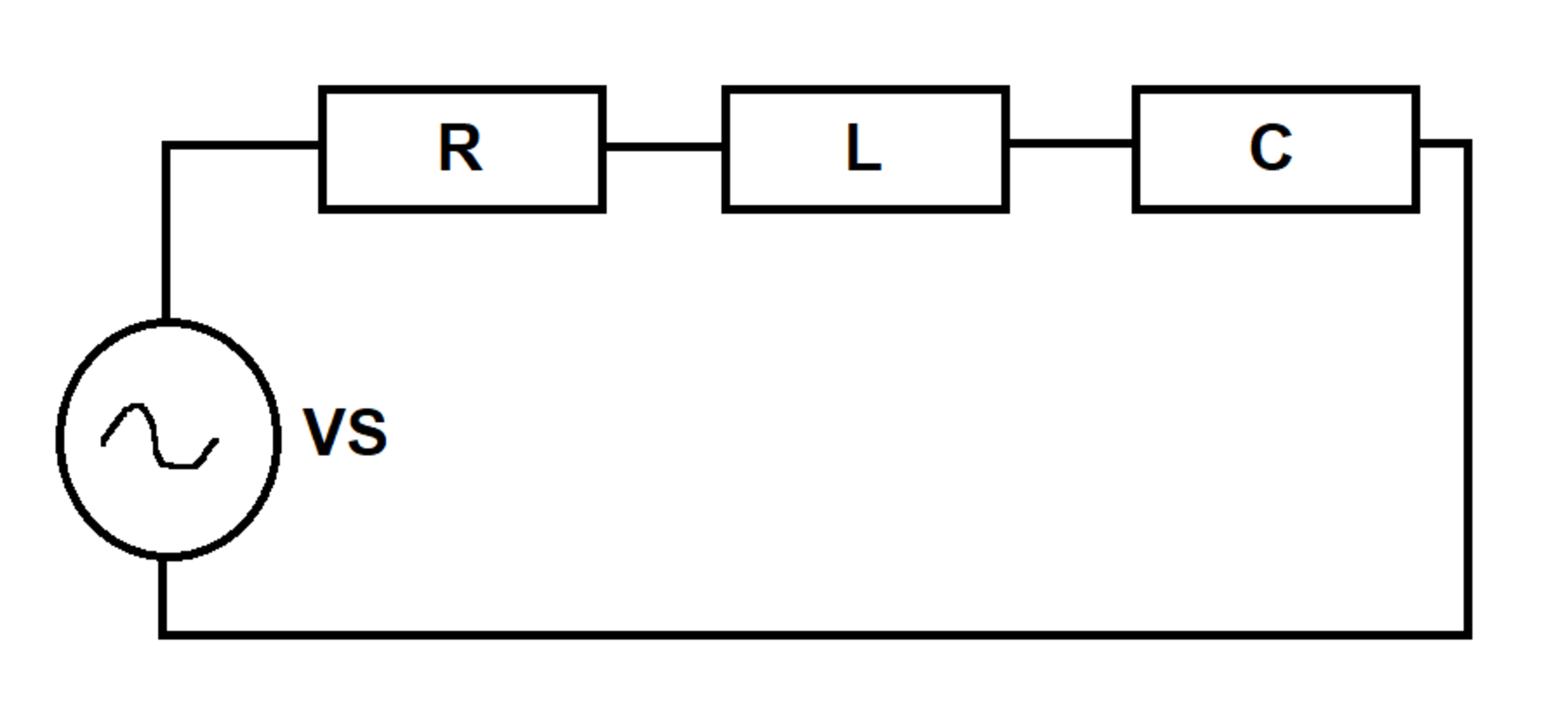
Resonant Circuit

The underlying concept of this problem is quite interesting. I was in fact thinking of posting something on resonance in the context of vibrations. Anyway, let the instantaneous charge on the capacitor be $Q$ and current through the circuit be $I$ . $I(0)=Q(0)=0$ . CIrcuit equation:

$\ddot{Q} + \dot{Q} + Q = \cos{t}+\sin{t}$

Using the 'D' operator notation, the following operations can be done (underlying theory left out)

$Q_{\mathrm{steady \ state}} = \frac{1}{D^2+D+1} (\cos{t}+\sin{t})$ Replacing $D^2$ by $-1$ : $\implies Q_{\mathrm{steady \ state}} =\frac{1}{D}(\cos{t}+\sin{t})$ $\implies DQ_{\mathrm{steady \ state}} = \cos{t}+\sin{t}$

$DQ_{\mathrm{steady \ state}}= I_{\mathrm{steady \ state}}$

$\implies I_{\mathrm{steady \ state}} = \cos{t}+\sin{t}$

So one can see that the steady state current and the voltage are the same, which means that while evaluating the final integral, the steady state responses cancel out leaving onely the transient response. After solving the characteristic equation of the circuit, the solution of the ODE governing charge is:

$Q = \sin{t}-\cos{t} +\mathrm{e}^{-t/2}\left(a \cos\left(\frac{t\sqrt{3}}{2}\right) + b \sin\left(\frac{t\sqrt{3}}{2}\right)\right)$

Solving for $a$ and $b$ by applying initial conditions and then differentiating leads to:

$I =\cos{t}+\sin{t} - \mathrm{e}^{-t/2}\left( \cos\left(\frac{t\sqrt{3}}{2}\right) + \frac{1}{\sqrt{3}} \sin\left(\frac{t\sqrt{3}}{2}\right)\right)$

$\int_{0}^{\infty} (V_S - RI) \ dt = \int_{0}^{\infty} \mathrm{e}^{-t/2}\left( \cos\left(\frac{t\sqrt{3}}{2}\right) + \frac{1}{\sqrt{3}} \sin\left(\frac{t\sqrt{3}}{2}\right)\right)\ dt =\boxed{1}$

This result can be generalized. If the exciting frequency matches the natural frequency of the system, in the presence of damping (resistance), then the steady state voltage across the resistor (or damping force, depending on the system) will cancel out the exciting voltage (or force). If there is no damping, then the system will evolve in an unbounded fashion as is the case in undamped resonant systems.

Note: the 'D' operator indicates differentiation with respect to time. Any function of $D$ namely $f(D)$ can be thought of as an operator applied to a function of time, which would yield another function. This approach is different from my standard Laplace transform method.