Reuleaux Triangle in a Square
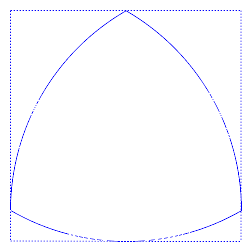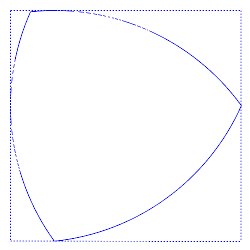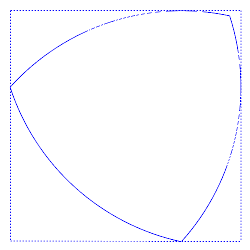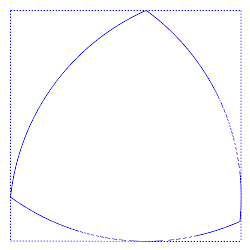
Shown at right is a Reuleaux triangle rotating inside a unit square, always being in touch with all 4 edges of the square.
The total area covered by the Reuleaux triangle as it rotates is a + b 3 + c π , where a , b , and c are rational numbers.
Find a b c .
Image from Wikimedia Commons
The answer is -1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Forgive my ignorance. The article states:
By the Blaschke–Lebesgue theorem, the Reuleaux triangle has the smallest possible area of any curve of given constant width. This area is
( 2 1 ( π − 3 ) ) s 2 ≈ 0 . 7 0 4 7 7 s 2 Would not the area be: 2 1 ( π − 3 ) Your answer: − 3 + 2 3 + 6 π ≈ 0 . 9 9 Is not this number too large?
Log in to reply
That is the area of the Reuleaux triangle itself. In this question I am asking for the area it traces out when it rotates inside a square. Sorry if that wasn’t particularly clear.
Let's make the unit square the square defined by the points (0,0), (0,1), (1,0) and (1,1).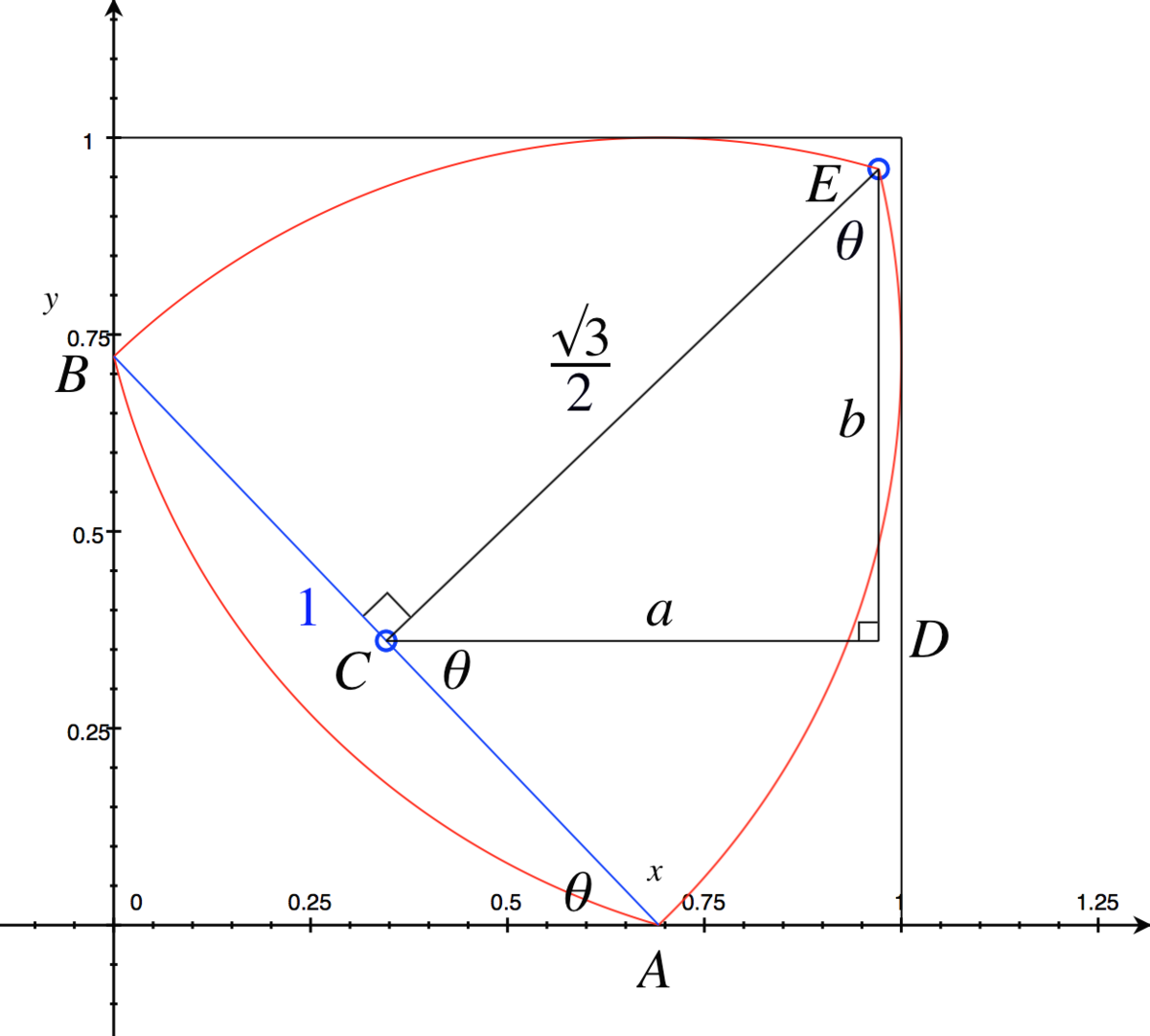 We can see that since the Reuleaux triangle was a constant width of 1, the line AB must have a length of 1. This means A has coordinates
(
cos
θ
,
0
)
and B has coordinates
(
0
,
sin
θ
)
. As these two points move along the bottom and left sides of the square, the third corner E traces out an elliptical path which we need to determine the equation of.
We can see that since the Reuleaux triangle was a constant width of 1, the line AB must have a length of 1. This means A has coordinates
(
cos
θ
,
0
)
and B has coordinates
(
0
,
sin
θ
)
. As these two points move along the bottom and left sides of the square, the third corner E traces out an elliptical path which we need to determine the equation of.
I will do everything in terms of the parameter θ .
C is the midpoint of AB, and so C has coordinates: C = ( 2 cos θ , 2 sin θ ) △ A B E , the triangle created by connecting the points of the Reuleaux triangle with straight lines, is an equilateral triangle with side lengths of 1. This means CE, the perpendicular height where the base is AB, has a length of 2 3 . D is a point directly across from C and directly below E, we can easily prove by alternate angles and angle sum of a triangle that ∠ C E D = θ . This is all shown in the digram.
In triangle ABE: sin θ a = 3 / 2 a = 2 3 sin θ cos θ b = 3 / 2 b = 2 3 cos θ Now we can add these components of CE to the coordinates of C to determine the coordinates of E: E = ( 2 cos θ + a , 2 sin θ + b ) E = ( 2 3 sin θ + cos θ , 2 3 cos θ + sin θ ) Now we can eliminate the parameter and get an equation for x in terms of y: 3 y − x = 2 3 cos θ + 3 sin θ − 2 3 sin θ + cos θ = 2 2 cos θ = cos θ 3 x − y = 2 3 sin θ + 3 cos θ − 2 3 cos θ + sin θ = 2 2 sin θ = sin θ ( 3 y − x ) 2 + ( 3 x − y ) 2 3 y 2 − 2 3 x y + x 2 + 3 x 2 − 2 3 x y + y 2 4 y 2 − 4 3 x y + 4 x 2 − 1 y 2 − 3 x y + x 2 − 4 1 y y = cos 2 x + sin 2 x = 1 = 0 = 0 = 2 3 x ± 3 x 2 − 4 ( x 2 − 4 1 ) = 2 3 x ± 1 − x 2 The graph is an ellipse, but since we only want the top right corner of the ellipse, we only consider the positive part of the ± , so y = 2 3 x + 1 − x 2 Before we can make an integral, we need to find the terminals. These are the points where the ellipse touches the edges of the square, so the upper bound is obviously 1. For the lower bound, we need to look at where y=1 and find the corresponding x coordinate. y = 1 2 3 cos θ + sin θ = 1 cos ( θ − 6 π ) = 1 θ = 6 π x = 2 3 sin 6 π + cos 6 π x = 2 2 3 + 2 3 x = 2 3 Now we can make an integral to determine the area. Since the area is in the top right corner of the square, I'm going to move it to the bottom right corner so that it is touching the x axis by integrating 1 minus the function instead. = = = = = = = = ∫ 2 3 1 1 − 2 3 x + 1 − x 2 d x ∫ 2 3 1 1 − 2 3 x d x − ∫ 2 3 1 2 1 − x 2 d x [ x − 4 3 x 2 ] 2 3 1 − ∫ 3 π 2 π 2 1 − sin 2 u cos u d u (letting x=sinu) ( 1 − 4 3 ) − ( 2 3 − 1 6 3 3 ) − ∫ 3 π 2 π 2 cos 2 u d u 1 − 1 6 9 3 − ∫ 3 π 2 π 4 cos 2 u + 1 d u 1 − 1 6 9 3 − [ 8 sin 2 u + 4 u ] 3 π 2 π 1 − 1 6 9 3 − ( 8 sin π + 8 π ) + ( 8 sin 3 2 π + 1 2 π ) 1 − 1 6 9 3 − 8 π + 1 6 3 + 1 2 π 1 − 2 3 − 2 4 π This is the area not covered by the Reuleaux triangle in one of the corners, so we now need to multiply it by 4 and subtract it from the area of the square: A = 1 2 − 4 ( 1 − 2 3 − 2 4 π ) = 1 − 4 + 2 3 + 6 π = − 3 + 2 3 + 6 π So a = − 3 , b = 2 and c = 6 1 , so the answer is − 3 × 2 × 6 1 = − 1