Revenge of the colourful Sangaku

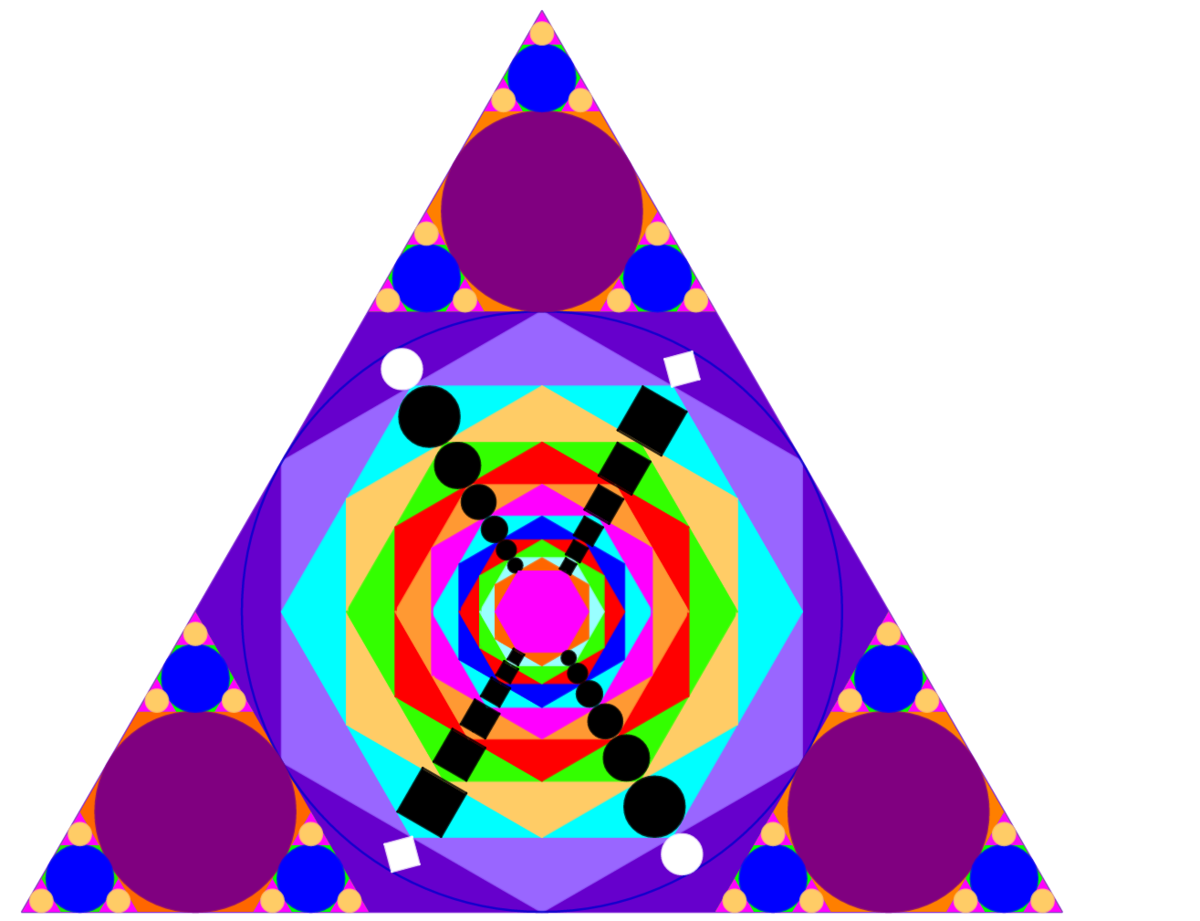
The diagram shows an equilateral triangle with side 1. This problem was made with the help of Eléa my favourite student.

• The pattern of inscribed circles (top, left and right) is repeated infinitely. The incircle of the big triangle is excluded from this pattern. The area of those circles is noted : $\boxed{β}$
• In the central part of the largest triangle we see that its incircle circumscribes an hexagon. This hexagon circumscribes a smaller hexagon; each vertex of the smaller hexagon is the middle of each side of the bigger hexagon. This pattern is repeated infinitely. The non-overlapping area of those hexagons forms an infinite number of isosceles triangles. We use one row of isosceles triangles to inscribe a black square each time. We name the total area of the infinite black squares : $\boxed{α}$
• We use another row of isosceles triangle to inscribe a black circle each time, infinitely. We note their total area : $\boxed{γ}$
• The two white circles are the biggest circles we can inscribe between the incircle of the big triangle and the largest hexagon. We note the area of the two white circles : $\boxed{ϕ}$
• The two white squares are inscribed between the incircle of the largest triangle and the largest hexagon. We note the area of the two white squares : $\boxed{θ}$

• THE QUESTION :
• Evaluate : $\boxed{\frac{α \times θ}{ϕ \times γ}+β}$
• The answer can be written in its simplest form as $\boxed{\frac{a+b\sqrt{c}}{e \times π^{f}}+\frac{π}{d}}$
• Calculate the value $\boxed{k=\sqrt[3]{a-\frac{b}{c}+f \times \ e \lfloor{π}\rfloor-\frac{d}{\lceil{π}\rceil}}}$
• Finally, what is the sum (rounded to the nearest integer) of all the solutions to $\boxed{2cos(2x)=-\sqrt{2}}$ if $\boxed{\frac{-kπ}{5}<x<π(3+k)}$