Revenge of the Deadly Sangaku
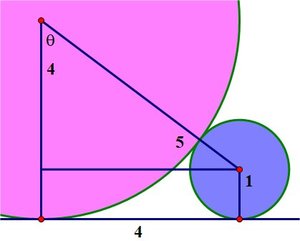
The diagram shows a portion of a purple circle with radius 4 and a blue circle of radius 1 tangent to each other and tangent to a black line. The space between the two circles and the black line is packed with circles in a certain pattern. The pattern continues to infinity.
Question : What percentage of the area limited by the blue circle, the purple circle and the black line is white? You may round your answer to the nearest integer.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
-
To solve this problem we need to calculate the area limited by the blue circle, the purple circle and the black line :
The required area is equal to : 2 3 × 4 + 4 × 1 − 3 6 0 ° 1 6 π × a r c c o s ( 3 / 5 ) − 3 6 0 ° π × ( 9 0 ° + a r c c o s ( 4 / 5 ) ) ≈ 1 , 4 7 4 4 9
- We then need Descartes' Circle Theorem to solve for the radii of the nested circles. We will deal with each type of circle separately, but let's solve first for the radius of the central red circle : 9 4
- We now deal with the light green circles on the left. Using Descartes' Circle Theorem we find that the radii follow this sequence : 4 1 , 2 5 4 , 9 1 , 4 9 4 . We can identify two groups of circles and write the infinite sum of their areas as follows:
- n = 2 ∑ ∞ π × n 4 1 ≈ 0 , 2 5 8 6 2 6
- n = 2 ∑ ∞ π × ( 2 n + 1 ) 4 1 6 ≈ 0 , 1 1 7 2 3 7
- Now we have to focus on the small light blue circles just above the green ones. Using Descartes' Circle Theorem we find that the radii follow this sequence : 1 3 1 , 2 1 1 , 3 1 1 , 4 3 1 We can easily deduce this formula to express the infinite sum of the circles' areas:
- n = 3 ∑ ∞ π × ( n 2 + n + 1 ) 2 1 ≈ 0 , 0 3 3 6 5
- Now let's look at the small brown circles below the green ones. Using Descartes' Circle Theorem we find that the radii follow this sequence : 4 9 4 , 8 1 4 , 1 2 1 4 , 1 6 9 4 We can easily deduce this formula to express the infinite sum of the circles' areas:
- n = 3 ∑ ∞ π × ( 2 n + 1 ) 4 1 6 ≈ 0 , 0 3 6 8 1
- Now let's look at the orange circles on the right side, we include the big red circle in the sequence. Using Descartes' Circle Theorem we find that the radii follow this sequence : 9 4 , 2 5 4 , 4 9 4 , 8 1 4 We can easily deduce this formula to express the infinite sum of the circles' areas:
- n = 1 ∑ ∞ π × ( 2 n + 1 ) 4 1 6 ≈ 0 , 7 3 7 7 9 8 3 4
- Now let's look at the black circles below the orange circles. Using Descartes' Circle Theorem we find that the radii follow this sequence : 1 6 1 , 3 6 1 , 6 4 1 , 1 0 0 1 We can easily deduce this formula to express the infinite sum of the circles' areas:
- n = 2 ∑ ∞ π × 1 6 n 4 1 ≈ 0 , 0 1 6 1 6 4
- Now let's look at the grey circles above the orange circles. Using Descartes' Circle Theorem we find that the radii follow this sequence : 1 9 1 , 3 9 1 , 6 7 1 , 1 0 3 1 We can easily deduce this formula to express the infinite sum of the circles' areas:
- n = 2 ∑ ∞ π × ( 4 n 2 + 3 ) 2 1 ≈ 0 , 0 1 2 1 4
- Now let's look at the light yellow circles above the red circle. Using Descartes' Circle Theorem we find that the radii follow this sequence : 7 1 , 5 7 4 , 2 4 1 , 1 4 5 4 , 5 1 1 , 2 7 3 4 We can identify two groups of circles and write the infinite sum of their areas as follows:
- n = 0 ∑ ∞ π × ( 5 n 2 + 1 2 n + 7 ) 2 1 ≈ 0 , 0 7 1 5 7 7
- n = 0 ∑ ∞ π × ( 2 0 n 2 + 6 8 n + 5 7 ) 2 1 6 ≈ 0 , 0 1 9 0 9
- Now let's look at the light blue circles left of the yellow circles. Using Descartes' Circle Theorem we find that the radii follow this sequence : 1 8 1 , 4 2 1 , 7 6 1 , 1 2 0 1 We can easily deduce this formula to express the infinite sum of the circles' areas:
- n = 0 ∑ ∞ π × ( 5 n 2 + 1 9 n + 1 8 ) 2 1 ≈ 0 , 0 1 2 5
- Now let's look at the green circles right of the yellow circles. Using Descartes' Circle Theorem we find that the radii follow this sequence : 8 1 4 , 1 7 7 4 , 3 1 3 4 , 4 8 9 4 We can easily deduce this formula to express the infinite sum of the circles' areas:
- n = 0 ∑ ∞ π × ( 2 0 n 2 + 7 6 n + 8 1 ) 2 1 6 ≈ 0 , 0 1 0 2 4 6
- Finally we add all the values and find that the area of the circles is 1 , 3 2 5 8 3 9 2
- So the white area represents : 1 , 4 7 4 4 9 1 0 0 ( 1 , 4 7 4 4 9 − 1 , 3 2 5 8 3 9 2 ) ≈ 1 0 %
To start with we calculate the area defined by the pink circle, the blue circle and the black line to be Δ 0 = 1 0 − 2 1 × 4 2 × θ − 2 1 × 1 2 × ( π − θ ) = 1 0 − 2 1 π − 2 1 5 θ where θ = tan − 1 3 4 . We now use Descartes's Theorem to calculate the radii of the various sequences of circles. This is most easily done using the quantity k = r 1 , where r is the radius of the circle. If a third circle is tangent to two mutually tangent circles and a mutually tangent line (and the circle is the smaller of the two options), then its k value is given by k 3 = k 1 + k 2 . If a fourth circle is tangent to three mutually tangent circles (and is the smaller of the two options), then its k value is k 4 = k 1 + k 2 + k 3 + 2 k 1 k 2 + k 1 k 3 + k 2 k 3 .
The k value of the pink circle is 4 1 , the k value of the blue circle is 1 , and the k value of the red circle is k X = 4 9 .
- the n th light green circle (bottom left) is bounded by the pink circle, the ( n − 1 ) st light green circle and the black line (the 0 th light green circle is the red circle), and so by induction we have k values k A ( n ) = 4 1 ( n + 3 ) 2 .
- the n th dark brown circle is bounded by the n th and ( n − 1 ) st light green circles and the black line, and so we have k values k B ( n ) = 4 1 ( 2 n + 5 ) 2 .
- the n th slate blue circle is bounded by the n th and ( n − 1 ) st light green circles and the pink circle, and so we have k values k C ( n ) = n 2 + 5 n + 7 .
- the n th orange circle is bounded by the blue circle, the ( n − 1 ) st orange circle (the red circle is the 0 th) and the black line, so we have k values k D ( n ) = 4 1 ( 2 n + 3 ) 2 .
- the n th black circle is bounded by the n th and ( n − 1 ) st orange circles and the black line, and so we have k values k E ( n ) = ( 2 n + 2 ) 2 .
- the n th grey circle is bounded by the n th and ( n − 1 ) st orange circles and the blue circle, and so we have k values k F ( n ) = 4 n 2 + 8 n + 7 .
- the n th yellow circle is bounded by the ( n − 1 ) st yellow circle (the red circle is the 0 th) and the pink and blue circles, so we have k values k G ( n ) = 4 1 ( 5 n 2 + 1 4 n + 9 ) .
- the n th light blue circle is bounded by the n th and ( n − 1 ) st yellow circles and the pink circle, so we have k values k H ( n ) = 5 n 2 + 9 n + 4 .
- the n th dark green circle is bounded by the n th and ( n − 1 ) st yellow circles and the blue circle, and so we have k values k I ( n ) = 5 n 2 + 9 n + 4 2 5 .
The total area that is coloured is thus Δ 1 = S X + S A + S B + S C + S D + S E + S F + S G + S H + S I where S X S A S B = k X 2 π = 8 1 1 6 π = n = 1 ∑ ∞ k A ( n ) 2 π = 1 6 π ( 9 0 1 π 4 − 1 2 9 6 1 3 9 3 ) = n = 1 ∑ ∞ k B ( n ) 2 π = 1 0 1 2 5 0 1 π ( 1 6 8 7 5 π 4 − 1 6 4 2 5 9 2 ) and so on. These sums can all be expressed exactly, but become increasingly complex, involving polygamma functions and the Euler-Mascheroni constant γ .
The percentage of white area remaining is thus Δ 0 Δ 0 − Δ 1 × 1 0 0 = 1 0 . 0 8 1 5 which, to the nearest integer, is 1 0 .
Thank you for posting !