Revenge of the deceiving Sangaku

Geometry Level pending

The diagram shows a blue scalene triangle. We extend each segment and draw three circles. Each circle is tangent to one of the triangle's sides and tangent to the extensions of the other two sides. At last, we join each center to form a bigger triangle in which the blue triangle is inscribed. The shortest distances between the sides of the blue triangle and its circumcenter are given : 17 8 \boxed{\frac{17}{8}} , 87 8 \boxed{\frac{87}{8}} , 105 8 \boxed{\frac{105}{8}}

  • The Question : We denote the purple area as α \boxed{α} and the blue area as β \boxed{β}
  • Find α β \boxed{\frac{α}{β}}
  • The answer can be expressed as a b \boxed{\frac{a}{b}} where a a and b b are coprime positive integers
  • Evaluate a − b 4 \boxed{\sqrt[4]{a-b}}


The answer is 3.

Valentin Duringer by Valentin Duringer , 30, Belgium

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Valentin Duringer
Jun 27, 2020
  • We can label the sides as a \boxed{a} , b \boxed{b} , c \boxed{c} and the circumradius as R \boxed{R}
  • From the law of cosines, we can write this first equality : c ² = a ² + b ² − 2 a b × c o s ( C ^ ) \boxed{c²=a²+b²-2ab \times cos(Ĉ)}
  • Now we need to express a \boxed{a} , b \boxed{b} , c \boxed{c} and c o s ( C ^ ) \boxed{cos(Ĉ)} in terms of R \boxed{R}
  • By the Intersecting chords theorem in the blue triangle's circumcircle we can express a \boxed{a} , b \boxed{b} , c \boxed{c} in terms of R \boxed{R}
  • c ² = 4 R ² − 289 16 \boxed{c²=4R²-\frac{289}{16}}
  • b ² = 4 R ² − 7569 16 \boxed{b²=4R²-\frac{7569}{16}}
  • a ² = 4 R ² − 11025 16 \boxed{a²=4R²-\frac{11025}{16}}
  • From the extended law of sine, we know that : R = c 2 s i n ( C ^ ) \boxed{R=\frac{c}{2sin(Ĉ)}} < = > \boxed{<=>} c o s ² ( C ^ ) = 1 − 4 R ² − 289 16 4 R ² \boxed{cos²(Ĉ)=1-\frac{4R²-\frac{289}{16}}{4R²}}
  • We can now substitute a ² \boxed{a²} , b ² \boxed{b²} , c ² \boxed{c²} in terms of R \boxed{R} in the first equality given by the law of cosines :
  • 4 R ² − 289 16 = 4 R ² − 7569 16 + 4 R ² − 11025 16 − 2 a b × c o s ( C ^ ) \boxed{4R²-\frac{289}{16}=4R²-\frac{7569}{16}+4R²-\frac{11025}{16}-2ab \times cos(Ĉ)}
  • < = > <=> 4 R ² − 18305 16 = 2 a b × c o s ( C ^ ) \boxed{4R²-\frac{18305}{16}=2ab \times cos(Ĉ)}
  • < = > <=> ( 4 R ² − 18305 16 ) ² = 4 a ² b ² × c o s ² ( C ^ ) \boxed{(4R²-\frac{18305}{16})²=4a²b² \times cos²(Ĉ)}
  • After squaring both side we can now substitute again a ² \boxed{a²} , b ² \boxed{b²} and c o s ² ( C ^ ) \boxed{cos²(Ĉ)} in terms of R \boxed{R}
  • ( 4 R ² − 18305 16 ) ² = 4 ( 4 R ² − 11025 16 ) ( 4 R ² − 7569 16 ) ( 1 − 4 R ² − 289 16 4 R ² ) \boxed{(4R²-\frac{18305}{16})²=4(4R²-\frac{11025}{16})(4R²-\frac{7569}{16})(1-\frac{4R²-\frac{289}{16}}{4R²})}
  • We solve the equation and find several values for R \boxed{R} , the only acceptable value is R = 145 8 \boxed{R=\frac{145}{8}}
  • We can now calculate a \boxed{a} , b \boxed{b} and c \boxed{c} :
  • a = 25 \boxed{a=25}
  • b = 29 \boxed{b=29}
  • c = 36 \boxed{c=36}
  • Finally we calculate the blue area : β = a b c 4 R = 25 × 29 × 36 4 × 145 8 = 360 \boxed{β=\frac{abc}{4R}=\frac{25 \times 29 \times 36}{4 \times \frac{145}{8}}=360}
  • Now we need to calculate the area of the bigger triangle, the three circles are actually the excircles of the blue triangle. One way to solve for the triangle's area is to use coordinate geometry.
  • We draw a coordinate system with the origin being point A of the blue triangle ABC with A B = c = 36 \boxed{AB=c=36} , A C = b = 29 \boxed{AC=b=29} , B C = a = 25 \boxed{BC=a=25}
  • Then we place A(0;0) B(36;0) and C(21;20)
  • We can label D \boxed{D} the center of the excircle tangent to side [AB]
  • We can label E \boxed{E} the center of the excircle tangent to side [BC]
  • We can label F \boxed{F} the center of the excircle tangent to side [AC]
  • Let's calculate the coordinates of D \boxed{D} , E \boxed{E} , F \boxed{F} , using this general formula is the quickest way:
  • x D = − c ⋅ x C + b ⋅ x B + a ⋅ x A − c + b + a = − 36 ⋅ 21 + 29 ⋅ 36 + 25 ⋅ 0 − 36 + 29 + 25 = 16 \boxed{x_D=\frac{-c\cdot x_C+b\cdot x_B+a\cdot x_A}{-c+b+a}=\frac{-36\cdot 21+29\cdot 36+25\cdot 0}{-36+29+25}=16}
  • y D = − c ⋅ y C + b ⋅ y B + a ⋅ y A − c + b + a = − 36 ⋅ 20 + 29 ⋅ 0 + 25 ⋅ 0 − 36 + 29 + 25 = − 40 \boxed{y_D=\frac{-c\cdot y_C+b\cdot y_B+a\cdot y_A}{-c+b+a}=\frac{-36\cdot 20+29\cdot 0+25\cdot 0}{-36+29+25}=-40}
  • x E = − a ⋅ x A + b ⋅ x B + c ⋅ x C − a + b + c = − 25 ⋅ 0 + 29 ⋅ 36 + 36 ⋅ 21 − 25 + 29 + 36 = 45 \boxed{x_E=\frac{-a\cdot x_A+b\cdot x_B+c\cdot x_C}{-a+b+c}=\frac{-25\cdot 0+29\cdot 36+36\cdot 21}{-25+29+36}=45}
  • y E = − a ⋅ y A + b ⋅ y B + c ⋅ y C − a + b + c = − 25 ⋅ 0 + 29 ⋅ 0 + 36 ⋅ 20 − 25 + 29 + 36 = 18 \boxed{y_E=\frac{-a\cdot y_A+b\cdot y_B+c\cdot y_C}{-a+b+c}=\frac{-25\cdot 0+29\cdot 0+36\cdot 20}{-25+29+36}=18}
  • x F = − b ⋅ x B + a ⋅ x A + c ⋅ x C − b + a + c = − 29 ⋅ 36 + 25 ⋅ 0 + 36 ⋅ 21 − 29 + 25 + 36 = − 9 \boxed{x_F=\frac{-b\cdot x_B+a\cdot x_A+c\cdot x_C}{-b+a+c}=\frac{-29\cdot 36+25\cdot 0+36\cdot 21}{-29+25+36}=-9}
  • y F = − b ⋅ y B + a ⋅ y A + c ⋅ y C − b + a + c = − 29 ⋅ 0 + 25 ⋅ 0 + 36 ⋅ 20 − 29 + 25 + 36 = 45 2 \boxed{y_F=\frac{-b\cdot y_B+a\cdot y_A+c\cdot y_C}{-b+a+c}=\frac{-29\cdot 0+25\cdot 0+36\cdot 20}{-29+25+36}=\frac{45}{2}}
  • We can now calculate the sides of the triangle DEF :
  • D E = ( x E − x D ) ² + ( y E − y D ) ² = 29 5 \boxed{DE=\sqrt{(x_E-x_D)²+(y_E-y_D)²}=29\sqrt{5}}
  • F E = ( x E − x F ) ² + ( y E − y F ) ² = 9 145 2 \boxed{FE=\sqrt{(x_E-x_F)²+(y_E-y_F)²}=\frac{9\sqrt{145}}{2}}
  • D F = ( x F − x D ) ² + ( y F − y D ) ² = 25 29 2 \boxed{DF=\sqrt{(x_F-x_D)²+(y_F-y_D)²}=\frac{25\sqrt{29}}{2}}
  • By Heron's formula we get the area of the triangle EDF which is 6525 4 \boxed{\frac{6525}{4}}
  • We then get the purple area by substraction α = 6525 4 − β = 5085 4 \boxed{α=\frac{6525}{4}-β=\frac{5085}{4}}
  • α β = 113 32 \boxed{\frac{α}{β}=\frac{113}{32}}
  • 113 − 32 4 = 81 4 = 3 \boxed{\sqrt[4]{113-32}=\sqrt[4]{81}=3}
2 Helpful 3 Interesting 2 Brilliant 0 Confused
David Vreken
Jul 13, 2020

Let the blue triangle have sides a a , b b , and c c and a circumradius of R R , and label it as follows:

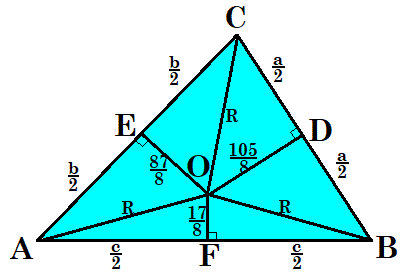
As given, let O D = 105 8 OD = \frac{105}{8} , O E = 87 8 OE = \frac{87}{8} , and O F = 17 8 OF = \frac{17}{8} . By the properties of a circumcircle , O D OD is the perpendicular bisector of B C BC , O E OE is the perpendicular bisector of A C AC , and O F OF is the perpendicular bisector of A B AB . By the Pythagorean Theorem on △ O D C \triangle ODC , △ O E A \triangle OEA , and △ O F B \triangle OFB :

( a 2 ) 2 + ( 105 8 ) 2 = R 2 (\frac{a}{2})^2 + (\frac{105}{8})^2 = R^2

( b 2 ) 2 + ( 87 8 ) 2 = R 2 (\frac{b}{2})^2 + (\frac{87}{8})^2 = R^2

( c 2 ) 2 + ( 17 8 ) 2 = R 2 (\frac{c}{2})^2 + (\frac{17}{8})^2 = R^2

The area of △ A B C \triangle ABC is β = A △ A B C = A △ O B C + A △ O A C + A △ O A B = 1 2 ⋅ 105 8 ⋅ a + 1 2 ⋅ 87 8 ⋅ b + 1 2 ⋅ 17 8 ⋅ c \beta = A_{\triangle ABC} = A_{\triangle OBC} + A_{\triangle OAC} + A_{\triangle OAB} = \frac{1}{2} \cdot \frac{105}{8} \cdot a + \frac{1}{2} \cdot \frac{87}{8} \cdot b + \frac{1}{2} \cdot \frac{17}{8} \cdot c , or:

16 β = 105 a + 87 b + 17 c 16\beta = 105a + 87b + 17c

and by the properties of a circumcircle:

4 β R = a b c 4\beta R = abc

These five equations solve to a = 25 a = 25 , b = 29 b = 29 , c = 36 c = 36 , R = 145 8 R = \frac{145}{8} , and β = 360 \beta = 360 .

The green circles are excircles and the purple and blue triangle is an excentral triangle with an area of α + β = a b c 2 r 2 s β \alpha + \beta = \frac{abc}{2r^2s}\beta . Substituting β = r s \beta = rs and s = 1 2 ( a + b + c ) s = \frac{1}{2}(a + b + c) and rearranging gives:

α = ( a + b + c ) a b c 4 β − β = 5085 4 \alpha = \frac{(a + b + c)abc}{4\beta} - \beta = \frac{5085}{4}

Therefore, α β = 113 32 \frac{\alpha}{\beta} = \frac{113}{32} , so a = 113 a = 113 , b = 32 b = 32 , and a − b 4 = 3 \sqrt[4]{a - b} = \boxed{3} .

0 Helpful 0 Interesting 1 Brilliant 0 Confused

Much better than my solution !! Thank you !

Valentin Duringer - 11 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...