Revenge of the extremist Sangaku

Geometry Level pending

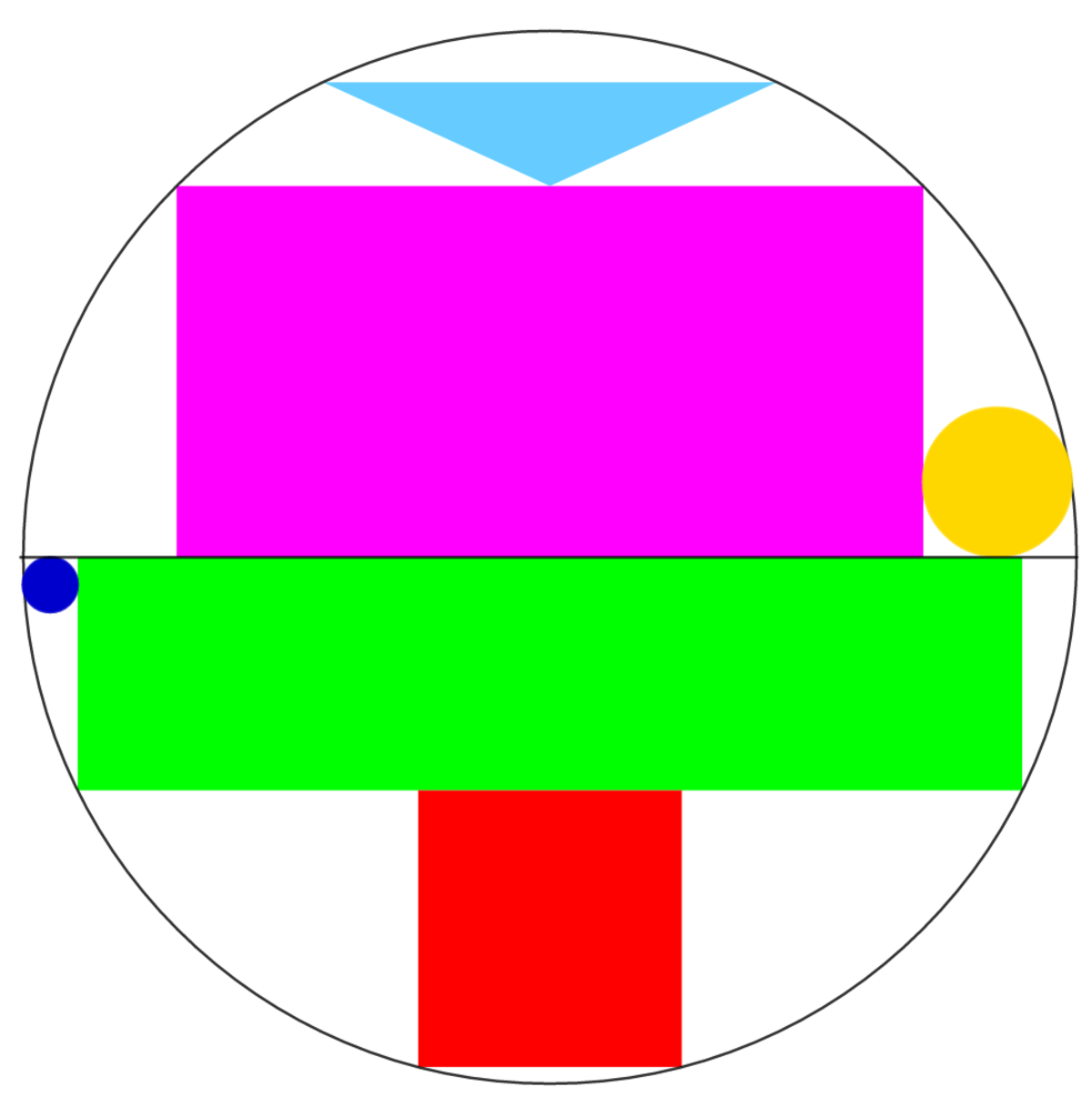
The diagram shows a circle of radius 1. We divide the circle into two semicircles. And we inscribe several figures:

The purple rectangle is the rectangle which has the maximum area possible that can be inscribed in the first semicircle.
The green rectangle is the rectangle which has the maximum perimeter that can be inscribed in the second semicircle.
The red square is inscribed between the circle and the green rectangle.
The blue triangle is the isosceles triangle which has the maximum area possible that can be inscribed between the purple rectangle and the circle.
The yellow circle is inscribed between the circle's diameter, the purple rectangle and the circle.
The blue circle is inscribed between the circle's diameter, the green rectangle and the circle.

The radius of the blue circle can be expressed as : $\boxed{\sqrt{a+\frac{b}{\sqrt{c}}}-\frac{a}{\sqrt{c}}-d}$ . Evaluate $\boxed{\gamma =a+b+c+d}$
The radius of the yellow circle can be expressed as : $\boxed{\sqrt{a+\sqrt{a}}-\frac{d}{\sqrt{a}}-d}$ . Evaluate $\boxed{\beta =a+d}$
The side of the red square can be expressed as : $\boxed{\frac{c\sqrt{e}-c}{b\sqrt{b}}}$ . Evaluate $\boxed{\alpha =b+e+c}$
The perimeter of the purple rectangle can be expressed as : $\boxed{f\sqrt{a}}$ . Evaluate $\boxed{\phi =f+a}$
The area of the green rectangle can be expressed as $\boxed{\frac{b}{c}}$ . Evaluate $\boxed{\lambda =b+c}$
The base of the blue isosceles triangle can be expressed as $\boxed{\frac{\sqrt{g-\sqrt{h}}}{a}}$ . Evaluate $\boxed{\theta =g+h+a}$

1 solution

Valentin Duringer
Jul 22, 2020

We draw a coordinate system and give the circle the equation $\boxed{x^{2}+y^{2}-1=0}$ . We are going to use this equation de write functions helping us to find the dimensions of every polygons.

$\color{#69047E}Purple$ $\color{#69047E}rectangle$ : We place a point $\boxed{M(x;y)}$ and a point $\boxed{N(-x;y)}$ on the circle. Then the length of the rectangle's base is $\boxed{2x}$ and since the two points are on the circle, we use its equation to express $\boxed{y}$ in terms of $\boxed{x}$ : $\boxed{x^{2}+y^{2}-1=0}$ $<=>$ $\boxed{y=\sqrt{1-x^2}}$
We conclude that the the area in terms of $\boxed{x}$ is $\boxed{A(x)=2x\sqrt{1-x^2}}$
We obtain the derivative : $\boxed{A'(x)=\frac{2-4x^2}{\sqrt{1-x^2}}}$ and we set the derivative to $0$ : $\boxed{\frac{2-4x^2}{\sqrt{1-x^2}}=0}$ $<=>$ $\boxed{x=\frac{\sqrt{2}}{2}}$
The perimeter is then : $\boxed{P(\frac{\sqrt{2}}{2})=4\cdot \frac{\sqrt{2}}{2}+2\cdot \sqrt{1-\left(\frac{\sqrt{2}}{2}\right)^2}=3\sqrt{2}}$
$\boxed{\phi =f+a=3+2=5}$

$\color{#20A900}Green$ $\color{#20A900}rectangle$ : We use a similar method to get the perimeter in terms of $\boxed{x}$ :
$\boxed{P(x)=4x+2\sqrt{1-x^2}}$ then we obtain the derivative, set it equal to $0$ and get $\boxed{x=\frac{2}{\sqrt{5}}}$
Then its area is : $\boxed{A\left(\frac{2}{\sqrt{5}}\right)=2\cdot \frac{2}{\sqrt{5}}\cdot \sqrt{1-\left(\frac{2}{\sqrt{5}}\right)^2}=\frac{4}{5}}$
$\boxed{\lambda =b+c=4+5=9}$

$\color{#3D99F6}Blue$ $\color{#3D99F6}triangle$ : We us the same method and find that the base is equal to : $\boxed{\frac{\sqrt{7-\sqrt{17}}}{2}}$
$\boxed{\theta =g+h+a=7+17+2=26}$

$\color{#CEBB00}Yellow$ $\color{#CEBB00}circle$ : We use the pythagorean theorem : $\boxed{\left(1-r\right)^2=r^2+\left(\frac{\sqrt{2}}{2}+r\right)^2}$
$\boxed{r_y=\sqrt{2+\sqrt{2}}-\frac{1}{\sqrt{2}}-1}$
$\boxed{\beta =a+d=2+1=3}$

$\color{#3D99F6}Blue$ $\color{#3D99F6}circle$ : We use the same method and get :
$\boxed{r_b=\sqrt{2+\frac {4}{\sqrt{5}}}-\frac {2}{\sqrt{5}}-1}$
$\boxed{\gamma =a+b+c+d=2+4+5+1=12}$

$\color{#D61F06}Red$ $\color{#D61F06}square$ : We use the product of chords equality in a circle :
$\boxed{\frac{s^2}{4}=\left(s+1+\frac{1}{\sqrt{5}}\right)\cdot \left(2-s-1-\frac{1}{\sqrt{5}}\right)}$
$\boxed{s=\frac{4\sqrt{\:6}-4}{5\sqrt{5}\:}}$
$\boxed{\alpha =b+e+c=4+6+5=15}$