Reverse Monty?

Probability Level 3

You find yourself in a game show.

Behind each of two doors is a shiny new car. Behind the third door is a goat.

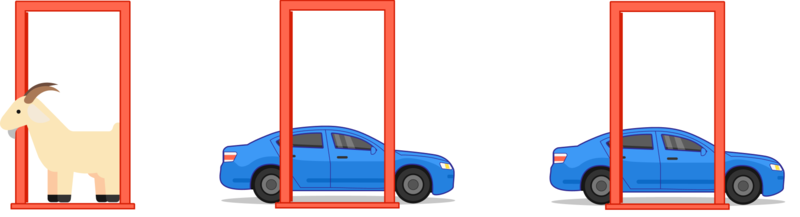
(and unlike these doors, you can't see what is behind them)

You pick one door at random without opening it, then the game show host, knowing what's left opens one revealing a car.

(It is known ahead of time that he always plays this way, since he can always find a door that will have a car behind it regardless of what your door has behind it)

He then offers you the chance to switch (to the only remaining door)..

If you do switch, what is the probability that you will win a car?

0

\frac{2}{3}

1

\frac{1}{2}

\frac{1}{3}

1 solution

Geoff Pilling
May 23, 2017

Lets enumerate the possibilities. The doors could have been arranged as follows:

And without loss of generality, lets suppose you pick the first door, so the three possibilities, with $\mathbf{{\color{#D61F06} red}}$ representing your choice, are:

$\mathbf{{\color{#D61F06} C}CG}$
$\mathbf{{\color{#D61F06} C}GC}$
$\mathbf{{\color{#D61F06} G}CC}$

In the first and second cases, when the host reveals the car, if you switch you will get the goat.

However, in the third case, when you switch, you will definitely choose a car.

Therefore, by switching you end up with only a $\boxed{\frac{1}{3}}$ chance of winning the car!

Nice variation of the Monty Hall problem! I looked at it as if getting the goat was a "win", which would set up the same dynamic as the original MH problem, and then taking the complement. Thus if you switch you would have a $2/3$ chance of "winning" the goat, which corresponds to a $1/3$ chance of actually winning the car.

Brian Charlesworth - 4 years ago

I looked at the complement too, but forgot to subtract from 1 before choosing the answer. I hate when that happens haha

Peter van der Linden - 4 years ago

Reverse Monty?

1 solution

0 pending reports