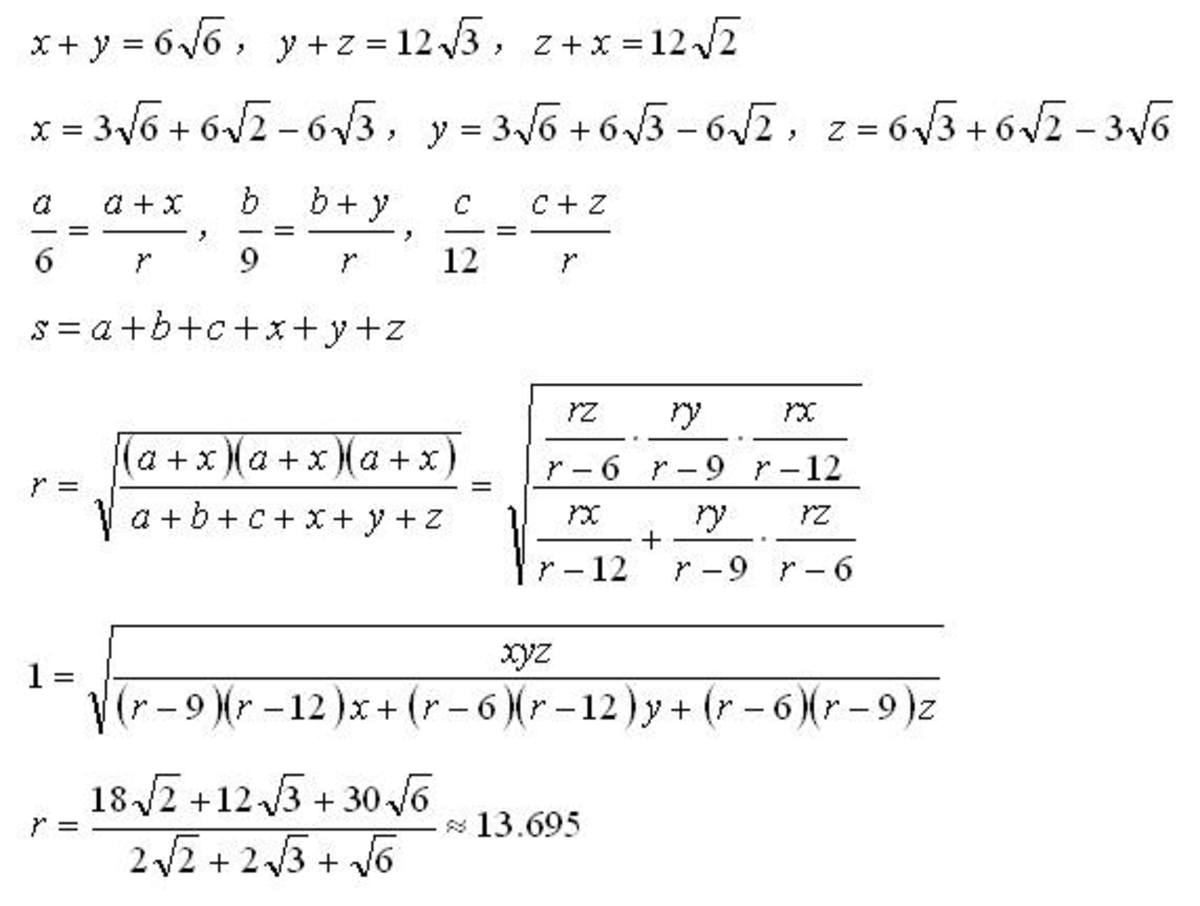Revival of Sangaku 2
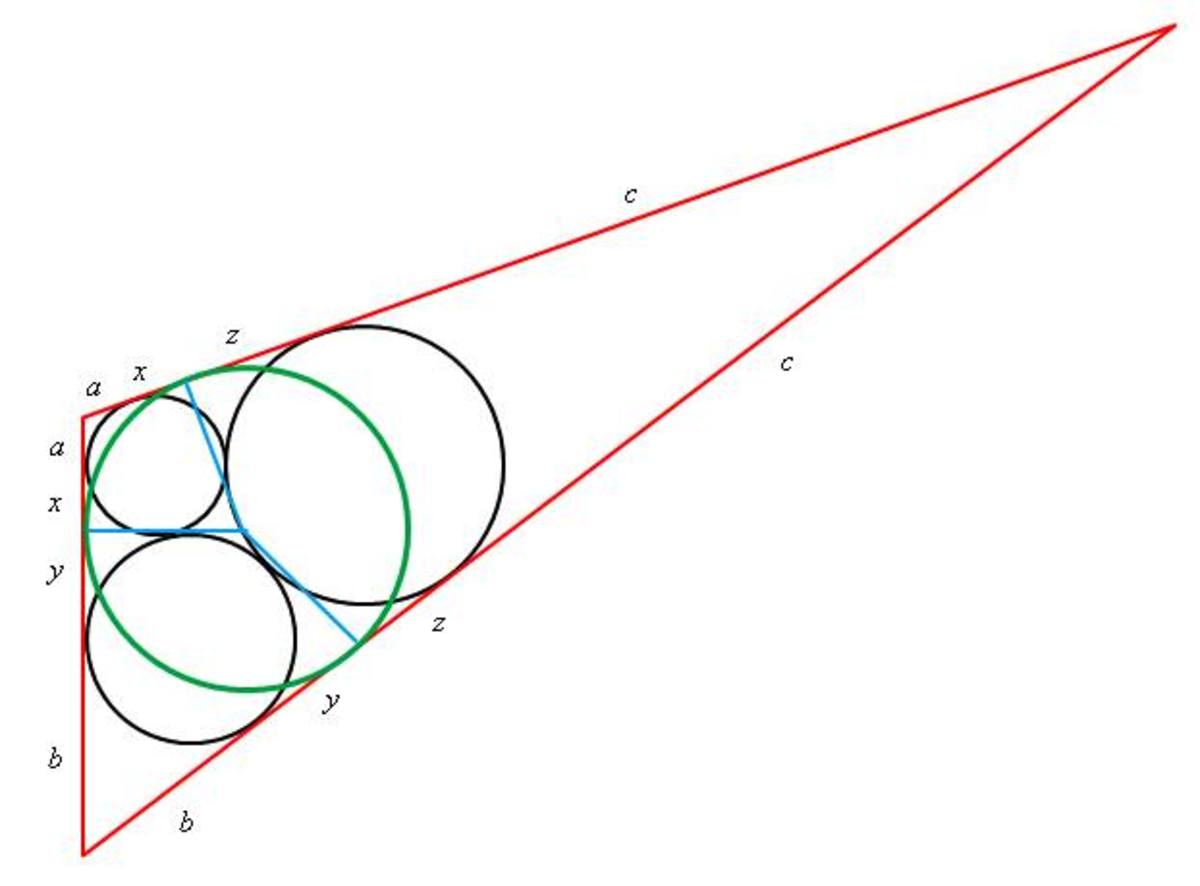
 Let there be three mutually tangent circles of radius 6, 9, and 12. If a triangle inscribes the three circles (diagram not to scale), calculate the radius of the triangle's incircle.
Let there be three mutually tangent circles of radius 6, 9, and 12. If a triangle inscribes the three circles (diagram not to scale), calculate the radius of the triangle's incircle.
The answer is 13.695.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I would be thrilled if you kindly post the detailed calculaton for arriving at r. Thanks,
A
B
C
i
s
t
h
e
e
n
v
e
l
o
p
i
n
g
Δ
.
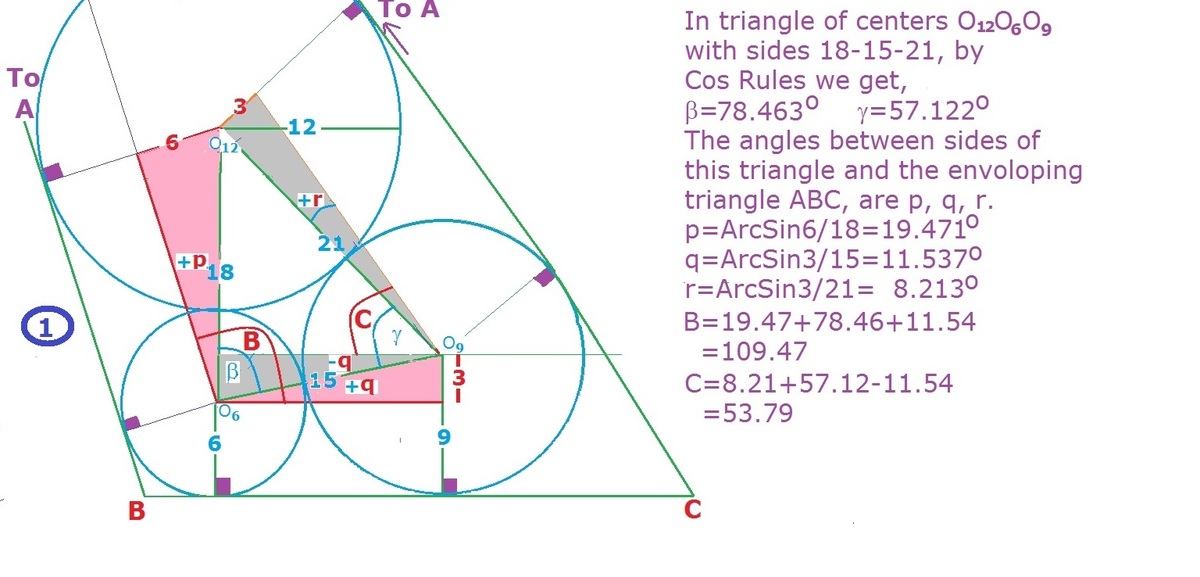
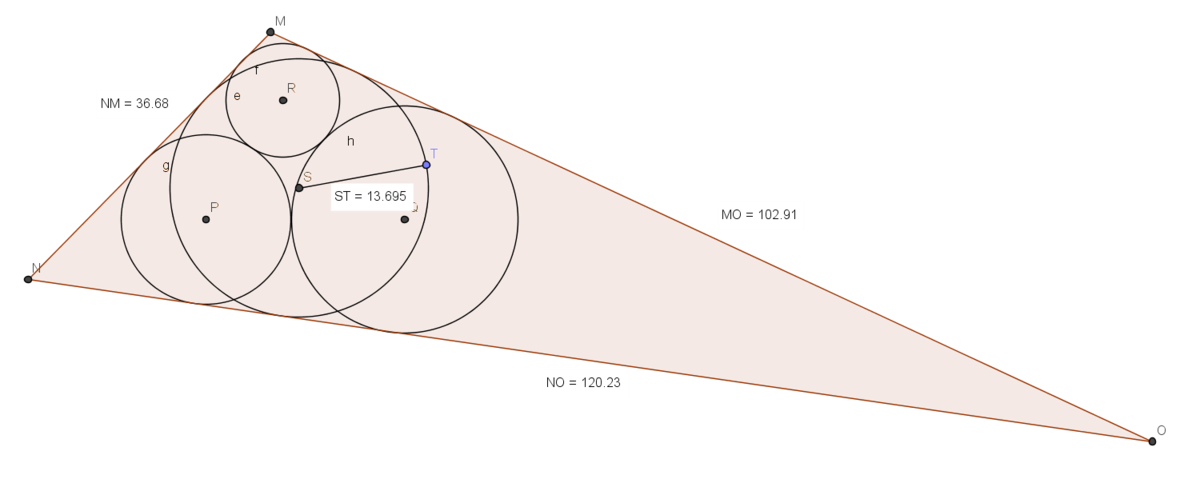
Based on the fact that the three given circles are on respective angle bisectors of ABC and its incircle is also where these three bisectors meet. So the centers of given circles are also on respective angle bisectors of ABC.
Thus from two centers
O
6
a
n
d
O
9
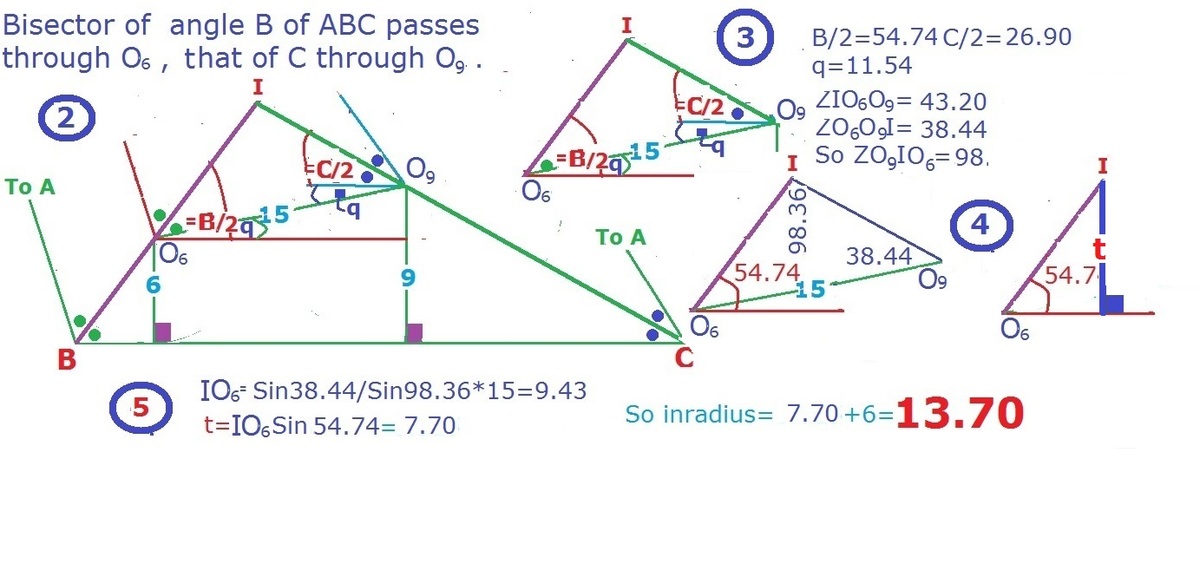
of the given circles we draw the angle bisectors to meet at incenter I of triangle ABC.
This two bisectors and the line joining their centers forms a ASA
Δ
I
O
6
O
9
.
From this triangle the distance of I from
O
6
is calculated and projected perpendicular to BC as t=7.70.
Add to t the distance of
O
6
from BC=6, we get the inradius required=
1
3
.
7
0
.
r=2√(xyz)/(√x+√y+√z -√(x+y+z)) where x=6, y=9 & z=12 Formula for in-radius as given by Fukagawa & Pedoe about which you can refer: http://mathworld.wolfram.com/MalfattiCircles.html
13.6953663887141951719809736008