Rhombicosidodecahedron
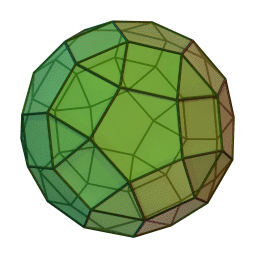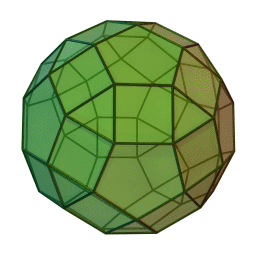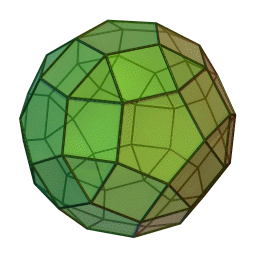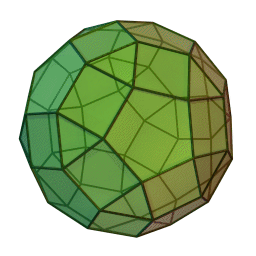
Let , , and be the number of vertices, edges, and faces on a rhombicosidodecahedron (a solid with 62 faces), respectively. Find .
Image Credit: Wikimedia Commons .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A dodecahedron has 2 0 vertices, 3 0 edges and 1 2 faces.
A isocahedron has 1 2 vertices, 3 0 edges, and 2 0 faces.
Hence, a rhombicosidodecahedron, combining both and adding some square faces (see helpful illustration provided above), has
2 1 ( 3 ⋅ 2 0 + 5 ⋅ 1 2 ) = 6 0 Vertices
2 ( 3 0 + 3 0 ) = 1 2 0 Edges
1 2 + 2 0 + 2 1 ( 6 0 ) = 6 2 Faces
Hence
V − E + F = 6 0 − 1 2 0 + 6 2 = 2
Of course we can use the general result of 2 of the Euler Characteristic for any convex polyhedron, but what's the fun in that?