Rhombicuboctahedral
A great rhombicuboctahedron is a polyhedron whose faces consist of 12 squares, 8 regular hexagons, and 6 regular octagons, as shown below.

Find the volume if all edges have unit length.
Give your answer to 1 decimal place.
The answer is 41.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A rhomicuboctahedron can be obtained from a cube whose faces lay on the same planes as the rhomibcuboctahedron octagonal faces. This can be accomplished by cutting away the vertices of the cube along the planes of the hexagonal faces and the edges along the planes of the square faces. The total volume to be removed can be subdivided into 44 pieces:
12 triangular prisms, one for each edge of the cube, formed by the plane of a square, the planes of the two adjacent octagons, and two planes normal to the square through the sides in common with the hexagons. Let V1 be one prism volume.
24 triangular pyramids, with bases in common with the prisms and vertices on the vertices of the cube. Let V2 be one triangular pyramid volume.
8 hexagonal pyramids, having the hexagons for bases and vertices in common with the cube. Three faces of a hexagonal pyramid are also skew faces of three triangular pyramids converging on the vertex. Let V3 be one hexagonal pyramid volume.
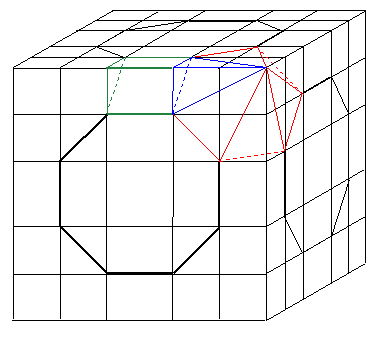
[The figure below shows a prism (green), a triangular pyramid (blue) and a hexagonal pyramid (red). Common edges are blue.]
Each prism has height 1; its base is an isosceles right-angled triangle with hypotenuse 1, so V1 = 1/2 x (1/sqrt(2))^2 x 1 = 1/4. The height of the triangular pyramid is 1/sqrt(2) + 1/sqrt(2) = sqrt(2), then V2 = 1/2 x (1/sqrt(2))^2 x sqrt(2) x 1/3 = sqrt(2)/12. The height of the hexagonal pyramid can be computed by applying twice the Pythagorean theorem: first the edge is computed as sqrt((sqrt(2)^2) + (1/sqrt(2))^2) = sqrt(5/2), then the height as sqrt((sqrt(5/2)^2 - 1) = sqrt(3/2). Since the base area is 6 x 1/2 x 1 x sqrt(3)/2 = 3sqrt(3)/2, V3 = 3sqrt(2)/4 follows.
The edge of the cube is 2sqrt(2) + 1; the volume of the rhombicuboctahedron is therefore (2sqrt(2) + 1)^3 - 12 x 1/4 - 24sqrt(2)/12 - 8 x 3sqrt(2)/4 = 22sqrt(2) + 25 -3 - 2sqrt(2) - 6sqrt(2) = 14sqrt(2) + 22 = ~41.79899...