Rhombus
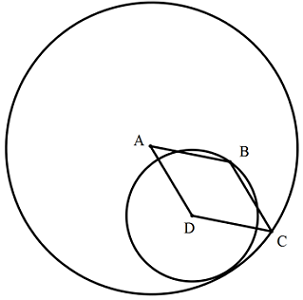
A rhombus has sides of length 10. A circle with center passes through (the opposite vertex.) Likewise, a circle with center passes through . If the two circles are tangent to each other, what is the area of the rhombus?
The answer is 75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let R be the radius of the large circle and r be the radius of the smaller circle.
By considering A D , we get that R − r = 1 0 .
By considering A B , we get that A B 2 = ( 2 A C ) 2 + ( 2 B D ) 2 , or that 4 0 0 = R 2 + r 2 .
Recall that the area of a rhombus is half the product of the diagonals, thus we are interested in the value of 2 R r . Squaring the first equation and subtracting the second, we obtain that 2 R r = ( R 2 + r 2 ) − ( R − r ) 2 = 4 0 0 − 1 0 0 = 3 0 0 . Thus, the area of the rhombus is 2 R r = 4 3 0 0 = 7 5 .