Rhombus is wonderful
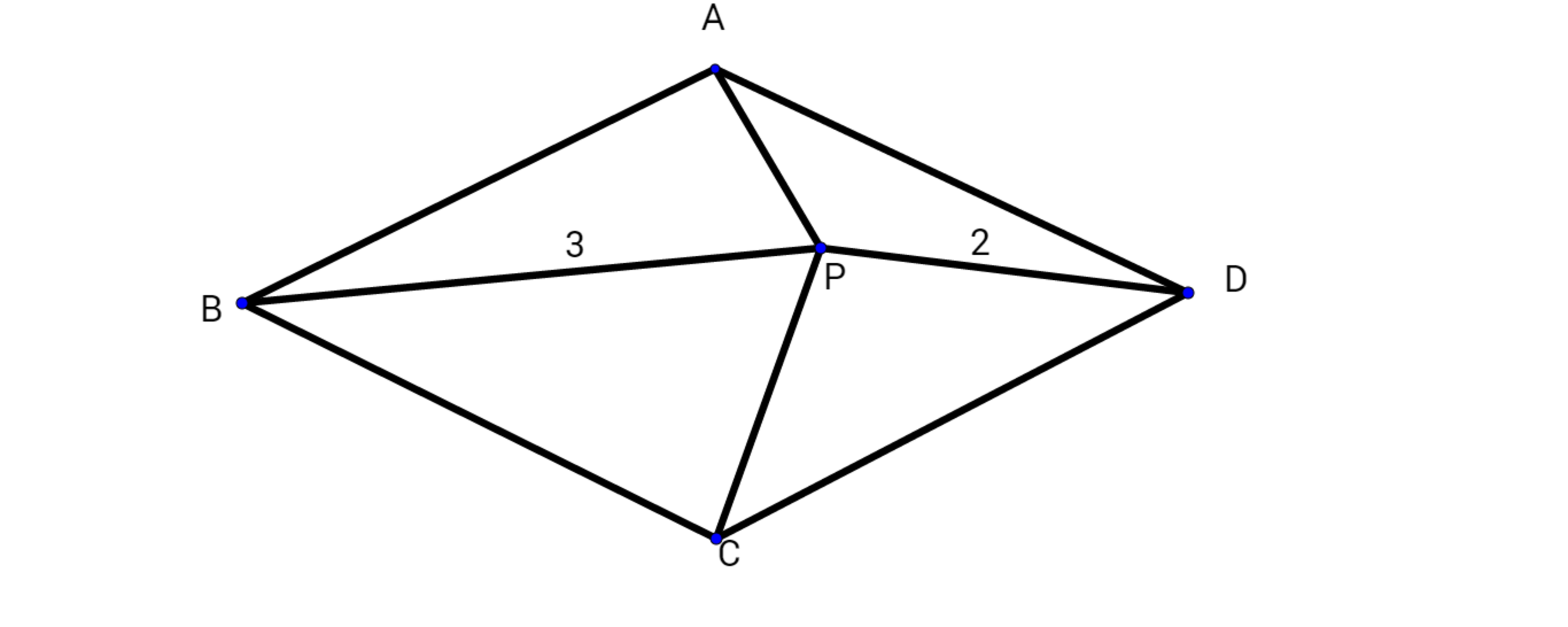 is a rhombus with
,
,
and
.
is a rhombus with
,
,
and
.
Find the difference between the lengths of and .
The answer is 1.527525.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First notice that Points A, P, C and B all lie on the same circle. Next, notice that Points A, D, C and the centroid of △ A B C lie on the same circle. I won't proof these since these are elementary.
Hence, the figure can be represented as: (Fig 1)
Now let's focus on triangle BPD (Fig 2)
Note that r is the radius of the circles.
From Fig 2:
Through △ B O P : 2 r cos θ 1 = 3
Through △ P O D and sine rule: r sin 2 θ 1 = 2 sin θ 2
Also through △ P O D and cosine rule: 4 + 3 r 2 − 8 r cos θ 2 = 0
Solving these equations give r = 3 2 2 and θ 1 = cos − 1 ( 2 2 2 9 )
Referring back to Fig 1 we get
∣ A P ∣ − ∣ P C ∣ = 2 r ( sin ( 3 0 ° + θ 1 ) − sin ( 3 0 ° − θ 1 ) ) = 2 r 3 sin θ 1 = 3 7 = 1 . 5 2 7 5 2 5 . . .