Rhombus Problem
The shorter diagonal, a , of a rhombus is x in. shorter than the longer diagonal, b . a and b are positive integers where a 2 + b 2 = 6 2 5 . If the sum of the area and perimeter of the rhombus is 200, what is the value of x ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
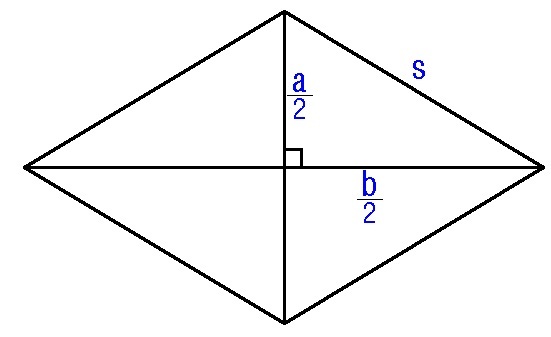 Let
a
be the shorter diagonal and
b
be the longer diagonal. By applying the Pythagorean Theorem,
s
=
(
2
a
)
2
+
(
2
b
)
2
=
4
a
2
+
4
b
2
=
2
1
a
2
+
b
2
=
2
1
6
2
5
=
1
2
.
5
Let
a
be the shorter diagonal and
b
be the longer diagonal. By applying the Pythagorean Theorem,
s
=
(
2
a
)
2
+
(
2
b
)
2
=
4
a
2
+
4
b
2
=
2
1
a
2
+
b
2
=
2
1
6
2
5
=
1
2
.
5
Solving for the perimeter
P = 4 s = 4 ( 1 2 . 5 ) = 5 0
Solving for the area
A = 2 1 a b = 2 1 ( a ) ( a + x ) = 2 1 a 2 + 2 1 a x
Adding the area and the perimeter
A + P = 2 0 0
2 1 a 2 + 2 1 a x + 5 0 = 2 0 0
After simplifying, we get
2 1 a 2 + 2 1 a x = 1 5 0 (equation 1)
We know that a 2 + b 2 = 6 2 5 , so
a 2 + ( a + x ) 2 = 6 2 5
After simplifying, we get
2 a 2 + 2 a x + x 2 = 6 2 5 (equation 2)
We multiply equation 1 by -4 then add to equation 2 to solve for x,
( 2 1 a 2 + 2 1 a x = 1 5 0 ) ( − 4 )
It becomes
− 2 a 2 − 2 a x = − 6 0 0
Add the above equation to equation 2, we get
x 2 = 2 5
Finally,
x = 5 i n c h e s
For a rhombus with diagonals a , b the area is 2 a b and the side length is 2 1 a 2 + b 2 .
We are thus given that 2 a b + 4 × 2 1 a 2 + b 2 = 2 0 0 ⟹ 2 a b + 2 × 6 2 5 = 2 0 0 ⟹ a b = 3 0 0 .
So then ( a + b ) 2 = a 2 + b 2 + 2 a b = 6 2 5 + 2 × 3 0 0 = 1 2 2 5 ⟹ a + b = 3 5 ⟹
a + a 3 0 0 = 3 5 ⟹ a 2 − 3 5 a + 3 0 0 = 0 ⟹ ( a − 1 5 ) ( a − 2 0 ) = 0 .
As a < b we thus have that ( a , b ) = ( 1 5 , 2 0 ) , and so x = b − a = 5 .