Rhombus Rhumble

Geometry Level pending

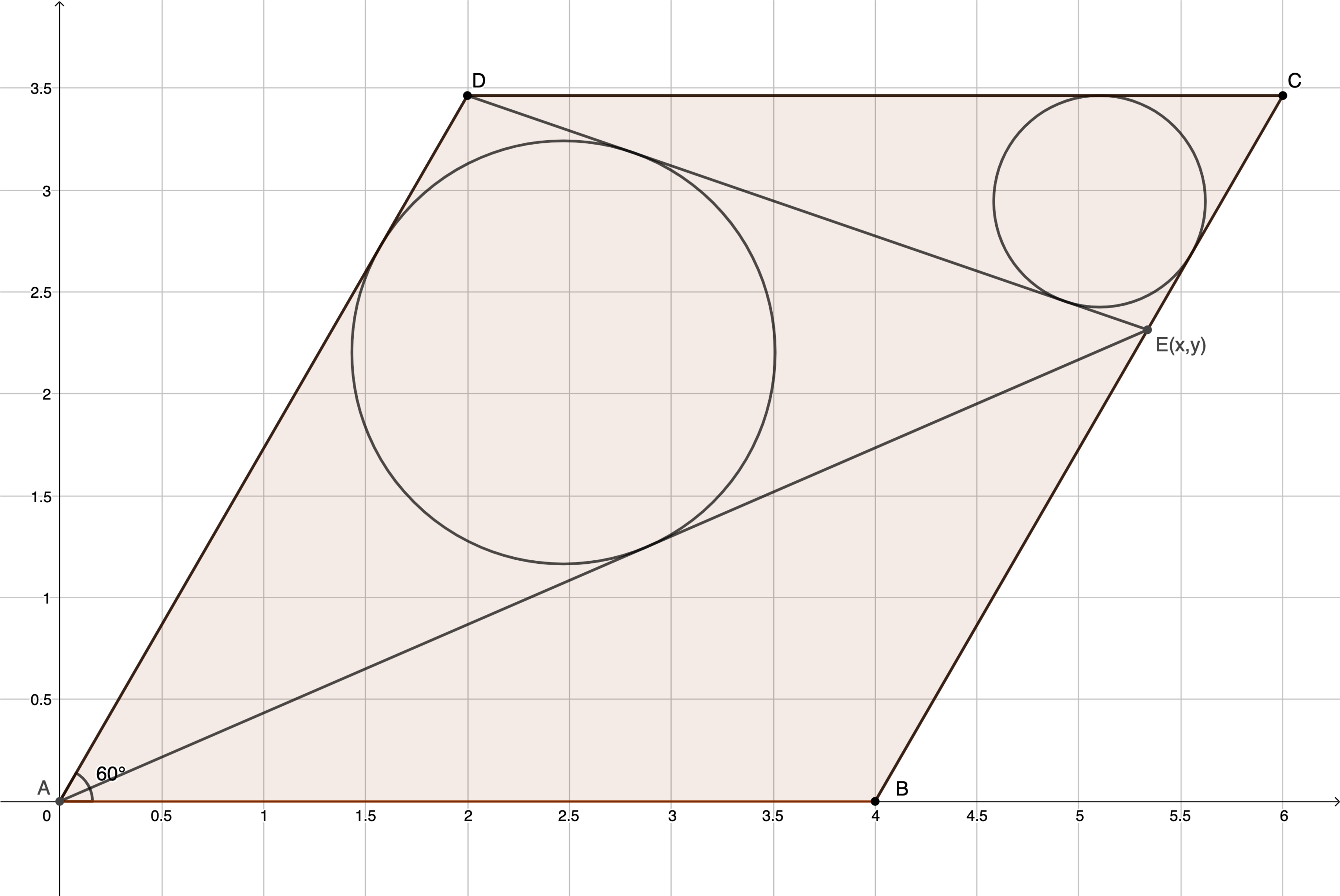
A B C D ABCD is a rhombus positioned on the coordinate plane with A A on the origin, as shown in the figure. Its inferior angle is 6 0 ∘ 60^\circ and the length of each side is 4 4 . E E is positioned on B C BC such that the radius of the larger circle is twice the radius of the smaller circle. Find the value of the x x -coordinate of E E . If it is a root of f ( x ) = a x 3 + b x 2 + c x + d + e f(x) = ax^3 + bx^2 + cx + d + e , where a > 0 a>0 , and gcd ( a , b , c , d , e ) = 1 (a,b,c,d,e)=1 , submit f ( 6 ) f(6) .


The answer is 13.

Fletcher Mattox by Fletcher Mattox , 72, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

David Vreken
May 22, 2021

Let the x x -coordinate of E E be x x .

Since A B = 4 AB = 4 and the exterior angle of ∠ A B E \angle ABE is 60 ° 60° , B E = 2 ( x − 4 ) = 2 x − 8 BE = 2(x - 4) = 2x - 8 , which means C E = B C − B E = 4 − ( 2 x − 8 ) = 12 − 2 x CE = BC - BE = 4 - (2x - 8) = 12 - 2x .

By the law of cosines on △ A B E \triangle ABE , A E = A B 2 + B E 2 − 2 ⋅ A B ⋅ B E ⋅ cos ⁡ A B E = 4 2 + ( 2 x − 8 ) 2 − 2 ⋅ 4 ⋅ ( 2 x − 8 ) ⋅ cos ⁡ 120 ° = 2 x 2 − 6 x + 12 AE = \sqrt{AB^2 + BE^2 - 2 \cdot AB \cdot BE \cdot \cos ABE} = \sqrt{4^2 + (2x - 8)^2 - 2 \cdot 4 \cdot (2x - 8) \cdot \cos 120°} = 2\sqrt{x^2 - 6x + 12} .

By the law of cosines on △ D C E \triangle DCE , D E = C D 2 + C E 2 − 2 ⋅ C D ⋅ C E ⋅ cos ⁡ D C E = 4 2 + ( 12 − 2 x ) 2 − 2 ⋅ 4 ⋅ ( 12 − 2 x ) ⋅ cos ⁡ 60 ° = 2 x 2 − 10 x + 28 DE = \sqrt{CD^2 + CE^2 - 2 \cdot CD \cdot CE \cdot \cos DCE} = \sqrt{4^2 + (12 - 2x)^2 - 2 \cdot 4 \cdot (12 - 2x) \cdot \cos 60°} = 2\sqrt{x^2 - 10x + 28} .

The area of △ A D E \triangle ADE is A △ A D E = 1 2 ⋅ b ⋅ h = 1 2 ⋅ 4 ⋅ 2 3 = 4 3 A_{\triangle ADE} = \frac{1}{2} \cdot b \cdot h = \frac{1}{2} \cdot 4 \cdot 2\sqrt{3} = 4\sqrt{3} .

The area of △ D C E \triangle DCE is A △ D C E = 1 2 ⋅ C D ⋅ C E ⋅ sin ⁡ D C E = 1 2 ⋅ 4 ⋅ ( 12 − 2 x ) ⋅ sin ⁡ 60 ° = 2 3 ( 6 − x ) A_{\triangle DCE} = \frac{1}{2} \cdot CD \cdot CE \cdot \sin DCE = \frac{1}{2} \cdot 4 \cdot (12 - 2x) \cdot \sin 60° = 2\sqrt{3}(6 - x) .

The inradius of △ A D E \triangle ADE is R = 2 A △ A D E A D + D E + A E = 2 ⋅ 4 3 4 + 2 x 2 − 10 x + 28 + 2 x 2 − 6 x + 12 = 4 3 2 + x 2 − 10 x + 28 + x 2 − 6 x + 12 R = \cfrac{2A_{\triangle ADE}}{AD + DE + AE} = \cfrac{2 \cdot 4\sqrt{3}}{4 + 2\sqrt{x^2 - 10x + 28} + 2\sqrt{x^2 - 6x + 12}} = \cfrac{4\sqrt{3}}{2 + \sqrt{x^2 - 10x + 28} + \sqrt{x^2 - 6x + 12}} .

The inradius of △ D C E \triangle DCE is r = 2 A △ D C E C D + C E + D E = 2 ⋅ 2 3 ( 6 − x ) 4 + ( 12 − 2 x ) + 2 x 2 − 10 x + 28 = 2 3 ( 6 − x ) 8 − x + x 2 − 10 x + 28 r = \cfrac{2A_{\triangle DCE}}{CD + CE + DE} = \cfrac{2 \cdot 2\sqrt{3}(6 - x)}{4 + (12 - 2x) + 2\sqrt{x^2 - 10x + 28}} = \cfrac{2\sqrt{3}(6 - x)}{8 - x + \sqrt{x^2 - 10x + 28}} .

Since the radius of the larger circle is twice the radius of the smaller circle, R = 2 r R = 2r , and this simplifies to:

4 3 2 + x 2 − 10 x + 28 + x 2 − 6 x + 12 = 2 ⋅ 2 3 ( 6 − x ) 8 − x + x 2 − 10 x + 28 \cfrac{4\sqrt{3}}{2 + \sqrt{x^2 - 10x + 28} + \sqrt{x^2 - 6x + 12}} = 2 \cdot \cfrac{2\sqrt{3}(6 - x)}{8 - x + \sqrt{x^2 - 10x + 28}}

8 − x + x 2 − 10 x + 28 = ( 6 − x ) ( 2 + x 2 − 10 x + 28 + x 2 − 6 x + 12 ) 8 - x + \sqrt{x^2 - 10x + 28} = (6 - x)(2 + \sqrt{x^2 - 10x + 28} + \sqrt{x^2 - 6x + 12}) (cross-multiply)

8 − x + x 2 − 10 x + 28 = 2 ( 6 − x ) + ( 6 − x ) x 2 − 10 x + 28 + ( 6 − x ) x 2 − 6 x + 12 8 - x + \sqrt{x^2 - 10x + 28} = 2(6 - x) + (6 - x)\sqrt{x^2 - 10x + 28} + (6 - x)\sqrt{x^2 - 6x + 12} (distribute)

( x − 5 ) x 2 − 10 x + 28 = 4 − x + ( 6 − x ) x 2 − 6 x + 12 (x - 5)\sqrt{x^2 - 10x + 28} = 4 - x + (6 - x)\sqrt{x^2 - 6x + 12} (rearrange)

( ( x − 5 ) x 2 − 10 x + 28 ) 2 = ( 4 − x + ( 6 − x ) x 2 − 6 x + 12 ) 2 ((x - 5)\sqrt{x^2 - 10x + 28})^2 = (4 - x + (6 - x)\sqrt{x^2 - 6x + 12})^2 (square both sides)

x 4 − 20 x 3 + 153 x 2 − 530 x + 700 = x 4 − 18 x 3 + 121 x 2 − 368 x + 448 + ( 2 x 2 − 20 x + 48 ) x 2 − 6 x + 12 x^4 - 20x^3 + 153x^2 - 530x + 700 = x^4 -18x^3 + 121x^2 - 368x + 448 + (2x^2 - 20x + 48)\sqrt{x^2 - 6x + 12} (expand)

− 2 x 3 + 32 x 2 − 162 x + 252 = ( 2 x 2 − 20 x + 48 ) x 2 − 6 x + 12 -2x^3 + 32x^2 - 162x + 252 = (2x^2 - 20x + 48)\sqrt{x^2 - 6x + 12} (simplify terms)

− 2 ( x − 3 ) ( x − 6 ) ( x − 7 ) = 2 ( x − 4 ) ( x − 6 ) x 2 − 6 x + 12 -2(x - 3)(x - 6)(x - 7) = 2(x - 4)(x - 6)\sqrt{x^2 - 6x + 12} (factor)

− ( x − 3 ) ( x − 7 ) = ( x − 4 ) x 2 − 6 x + 12 -(x - 3)(x - 7) = (x - 4)\sqrt{x^2 - 6x + 12} (cancel 2 ( x − 6 ) 2(x - 6) )

( − ( x − 3 ) ( x − 7 ) ) 2 = ( ( x − 4 ) x 2 − 6 x + 12 ) 2 (-(x - 3)(x - 7))^2 = ((x - 4)\sqrt{x^2 - 6x + 12})^2 (square both sides)

x 4 − 20 x 3 + 142 x 2 − 420 x + 441 = x 4 − 14 x 3 + 76 x 2 − 192 x + 192 x^4 - 20x^3 + 142x^2 - 420x + 441 = x^4 - 14x^3 + 76x^2 - 192x + 192 (expand)

6 x 3 − 66 x 2 + 228 x − 249 = 0 6x^3 - 66x^2 + 228x - 249 = 0 (simplify terms)

2 x 3 − 22 x 2 + 76 x − 83 = 0 2x^3 - 22x^2 + 76x - 83 = 0 (divide by 3 3 )

Therefore, f ( 6 ) = 2 ( 6 ) 3 − 22 ( 6 ) 2 + 76 ( 6 ) − 83 = 13 f(6) = 2(6)^3 - 22(6)^2 + 76(6) - 83 = \boxed{13} .

0 Helpful 0 Interesting 1 Brilliant 0 Confused

Thank you for slogging through all the algebra. Good job.

Fletcher Mattox - 3 weeks ago

Log in to reply

Thanks, and that was another fun question!

David Vreken - 3 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...