Rhombuses
From a central point, place n points 1 unit away and equally spaced. Construct a further point to make n rhombuses. Using two sides of each pair of neighboring rhombuses, create n more rhombuses. Keep creating rhombuses until you can't make any more (without overlapping.)
These are the constructions for n = 7 and n = 8 . The colors are only for visual effect.
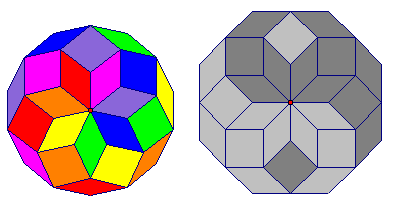
Find the area for n = 3 6 0 .
The answer is 41251.91405.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
It is the area of a regular 360-gon with side length 2.
Log in to reply
Oops. I guess I was doing it the hard way.
Log in to reply
But we still need to prove that it is a 360-gon.I think this part is harder.
Jeremy, put the Sin in that summation, you left that out.
But does such a figure exists?
Log in to reply
the 360-gon with 3 6 0 ⋅ 1 7 9 rhombuses does exist, even though it'll look like a pretty dense mat of lines, except where the rhombuses "open up" haflway between center and perimeter.
In fact, let me see if I put up a quickie approximation of what that would look like. Edit: Okay, see my solution with the figure.
I followed exactly this line of reasoning, by expressing the surfaces of every single rhombus as a sinusoidal function of the innermost angle of the quadrilateral, although I left the sum computing part to a C++ code (By innermost angles, I mean the angles you wrote as n*theta). But why did you end the sum with the n/2 = 180-th term? Wouldn't that mean adding the area of a non-existing rhombus with a 180° angle?
For even n , the final polygon is a regular n -polygon of side 2 . The area is, for side a = 2
A = 4 1 n a 2 C o t ( n π ) = 3 6 0 C o t ( 3 6 0 π ) ≈ 4 1 2 5 1 . 9 1 4
Jeremy's solution shows how and why the added rhombuses reach that final regular n -polygon.
Here's the 1 7 9 ⋅ 3 6 0 = 6 4 4 4 0 rhombuses put together. The Moire patterns is an artifact of having such a dense mat of lines in a rasterized display. But you can barely see the rhombuses "open up" in the middle zone between center and perimeter.

The central point of this partially constructed figure is at the far left. For any beginning angle θ , you can see the next set of rhombuses will have angle 2 θ , then 3 θ and so on. There will be ⌊ 2 n ⌋ sets of rhombuses (angles up to 1 8 0 degrees.)
The area of each rhombus with angle α is simply sin ( α ) so we just need to add up all the rhombuses. The general formula for any n is
n ∗ ∑ i = 1 ⌊ 2 n ⌋ sin ( i n 3 6 0 )
Using n = 3 6 0 gives the solution: 4 1 2 5 1 . 9 1 4 0 5
Which, not coincidentally is quite close to π 3 6 0 2