Ridiculous length!
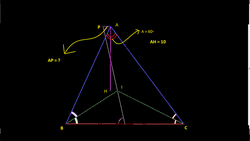 In acute
,
and
,
is the orthocentre,
is the incentre and
is the midpoint of
. The line passing through
and
intersects the straight line through
parallel to
at
. Suppose
and
.What is the numerical value of
?
In acute
,
and
,
is the orthocentre,
is the incentre and
is the midpoint of
. The line passing through
and
intersects the straight line through
parallel to
at
. Suppose
and
.What is the numerical value of
?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We produce A P to meet B C at X . Now △ A P I ∼ △ D I X . So,
D X A P = I X A I = C X A C = B X A B = C D + D X − B D + D X A C − A B = 2 A C − A B
Now, we know that sin ∠ B A C = sin ∠ C A B = 2 R , where R = circumradius of △ A B C
Therefore, A C = 2 R sin ∠ B and A B = 2 R sin ∠ C . So ,
A P = 2 R ( sin ∠ B − sin ∠ C ) × 2 1 = R × ( sin ∠ B − sin ∠ C )
We need to compute R . We take O , the circumcentre of △ A B C and drop O D ⊥ B C and join I and B . Using cos ∠ B O D = cos 6 0 ∘ = 2 1 and O D = 2 1 × A H = 5 , we have R = 1 0
Thus A P = R × ( sin ∠ B − sin ∠ C ) = 1 0 × 5 3 = 6