Inspired by Otto...Funny back to the future
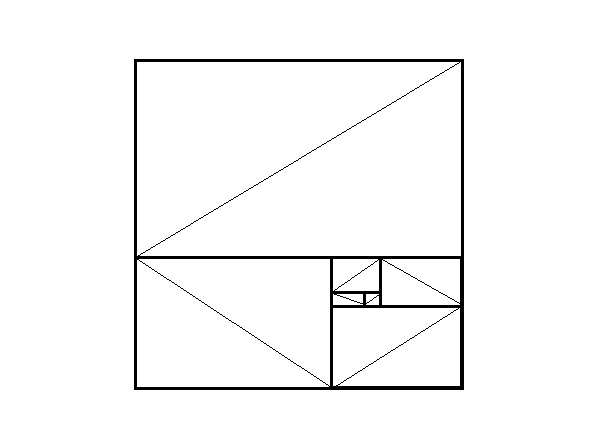 The Fibonacci sequence is defined with the recurrence relation
f
n
=
f
n
−
1
+
f
n
−
2
for
n
>
2
with initial terms
f
1
=
1
,
f
2
=
1
.
The Fibonacci sequence is defined with the recurrence relation
f
n
=
f
n
−
1
+
f
n
−
2
for
n
>
2
with initial terms
f
1
=
1
,
f
2
=
1
.
( 1 ⋅ 1 ) + ( 1 ⋅ 2 ) + ( 2 ⋅ 3 ) + ( 3 ⋅ 5 ) + … + ( f 2 0 1 2 ⋅ f 2 0 1 3 ) + ( f 2 0 1 3 ⋅ f 2 0 1 4 )
If the value of the expression above equals f n 2 , find the value of n .
The answer is 2014.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I cannot think of some really nice proof of the Lemma except using Binet's or Induction. Probably using Q-Matrix, but I don't know.
@Otto Bretscher Can you enlighten me?
f n f n + 2 = f n + 1 2 + ( − 1 ) n But f 1 f 3 = f 2 2 + ( − 1 ) 1
Log in to reply
I am sorry. But there I am using "pure" Fibonacci numbers where F 0 = F 1 = 1
Log in to reply
Okay .... it would be better if you had specified it in your solution.
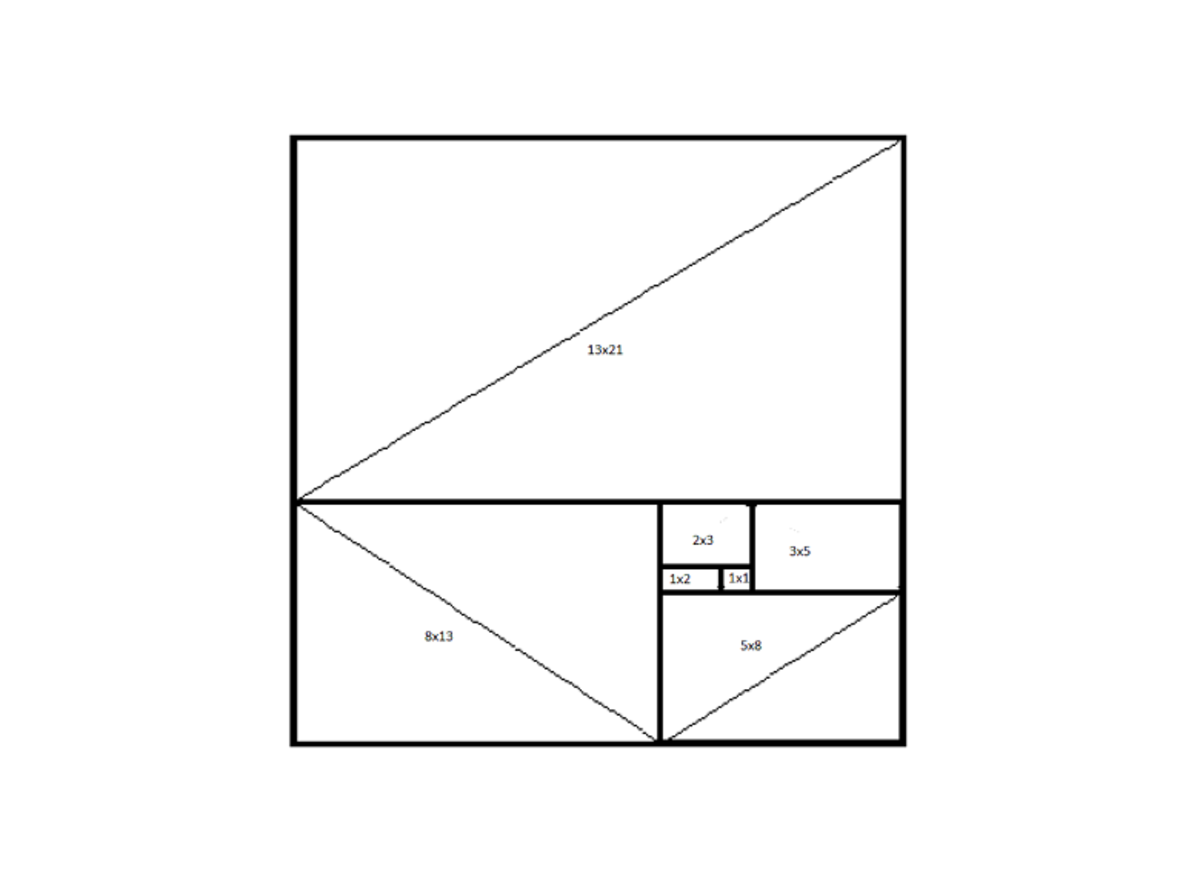
1 ⋅ 1 = 1 2 = f 1 ⋅ f 2
1 ⋅ 1 + 1 ⋅ 2 + 2 ⋅ 3 = 3 2 = f 1 ⋅ f 2 + f 2 ⋅ f 3 + f 3 ⋅ f 4
1 ⋅ 1 + 1 ⋅ 2 + 2 ⋅ 3 + 3 ⋅ 5 + 5 ⋅ 8 = 8 2 = f 1 ⋅ f 2 + f 2 ⋅ f 3 + f 3 ⋅ f 4 + f 4 ⋅ f 5 + f 5 ⋅ f 6
Using induction and seeing the picture above ( 1 ⋅ 1 ) + ( 1 ⋅ 2 ) + ( 2 ⋅ 3 ) + ( 3 ⋅ 5 ) + ... + ( f 2 0 1 2 ⋅ f 2 0 1 3 ) + ( f 2 0 1 3 ⋅ f 2 0 1 4 ) = f 2 0 1 4 2 ⇒ n=2014
The expression is basically:
f 1 ) ( f 2 ) + ( f 2 ) ( f 3 ) + ( f 3 ) ( f 4 ) + . . . . . . ( f 2 0 1 1 ) ( f 2 0 1 2 ) + ( f 2 0 1 2 ) ( f 2 0 1 3 ) + ( f 2 0 1 3 ) ( f 2 0 1 4 ) = f n 2
Which factors to;
f 2 ( f 1 + f 3 ) + f 4 ( f 3 + f 5 ) + f 6 ( f 5 + f 7 ) + . . . . . f 2 0 1 2 ( f 2 0 1 1 + f 2 0 1 3 ) + ( f 2 0 1 3 ) ( f 2 0 1 4 ) = f n 2
Based on the definition of Fibonacci sequence, f n = f n − 2 + f n − 1 ,
We have the related expression
( f 3 − f 1 ) ( f 1 + f 3 ) + ( f 5 − f 3 ) ( f 3 + f 5 ) + . . . . . . . ( f 2 0 1 3 − f 2 0 1 1 ) ( f 2 0 1 1 + f 2 0 1 3 ) + ( f 2 0 1 3 ) ( f 2 0 1 4 ) = f n 2
Which equals to:
( f 3 2 − f 1 2 ) + ( f 5 2 − f 3 2 ) + ( f 7 2 − f 5 2 ) + . . . . . . ( f 2 0 1 3 2 − f 2 0 1 1 2 ) + ( f 2 0 1 3 ) ( f 2 0 1 4 ) = f n 2
All the middle terms cancel out except for the f 2 0 1 3 2 :
− f 1 2 + f 2 0 1 3 2 + ( f 2 0 1 3 ∗ f 2 0 1 4 ) = f n 2
Which equals:
− 1 + f 2 0 1 3 ( f 2 0 1 3 + f 2 0 1 4 ) = f n 2
Which is the same as:
− 1 + f 2 0 1 3 ( f 2 0 1 5 ) = f n 2 (eq.1)
Using the identityof Fibonacci sequence f n + 1 ( f n − 1 ) − f n 2 = ( − 1 ) n and let n = 2 0 1 4 :
f 2 0 1 3 ( f 2 0 1 5 ) − f 2 0 1 4 2 = ( − 1 ) 2 0 1 4 = 1
Thus f 2 0 1 3 ( f 2 0 1 5 ) = 1 + f 2 0 1 4 2
Substitute into the original equation:
− 1 + 1 + f 2 0 1 4 2 = f n 2
n = 1 ∑ 2 0 1 3 f n f n + 1 = n = 1 ∑ 2 0 1 3 ( f n + 1 − f n − 1 ) f n + 1
n = 1 ∑ 2 0 1 3 f n + 1 2 − f n − 1 f n + 1
Lemma : f n f n + 2 = f n + 1 2 + ( − 1 ) n
Using this,
n = 1 ∑ 2 0 1 3 f n + 1 2 − f n 2 − ( − 1 ) n
Now, this easily telescopes to
f 2 0 1 4 2 − 1 + 1 = f 2 0 1 4 2