Riding round and round
A motorbike starts from rest at time and begins to accelerate around a circular track as shown in the figure below. Eventually, at time the motorbike reaches the maximum velocity possible without slipping off the track. What's the minimum length in meters the motorbike must travel between and ?
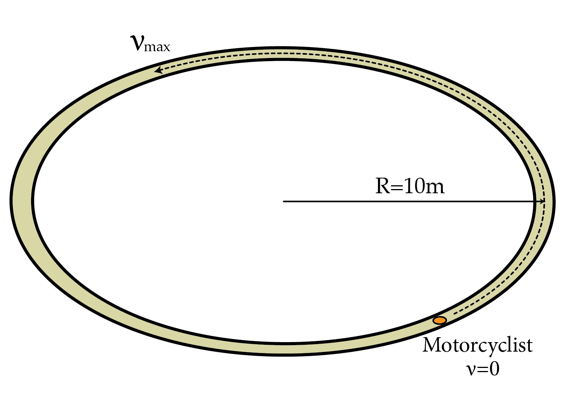
Details and assumptions
- Assume that the friction coefficient everywhere on the race track is the same.
- The motorbike wheels never slip on the track as it accelerates.
The answer is 7.85.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The maximum friction force is F o . The angle between the friction force and the velocity of the motorbike is α . The angle of the arc the motorbike has traveled on the track is θ .
In the tangent direction:
m d t d v = F o cos α
In the radial direction:
m R v 2 = F o sin α ⇒ R 2 m v d t d v = F o cos α d t d α
Divide the second equation by the first equation and we get:
R 2 v = d t d α
We can now substitute v / R = d θ / d t to get d θ = d α / 2 .
As the angle α changes from 0 to π / 2 , the arc the motorbike will travel is s = θ R = π R / 4 = 7 . 8 5 m .